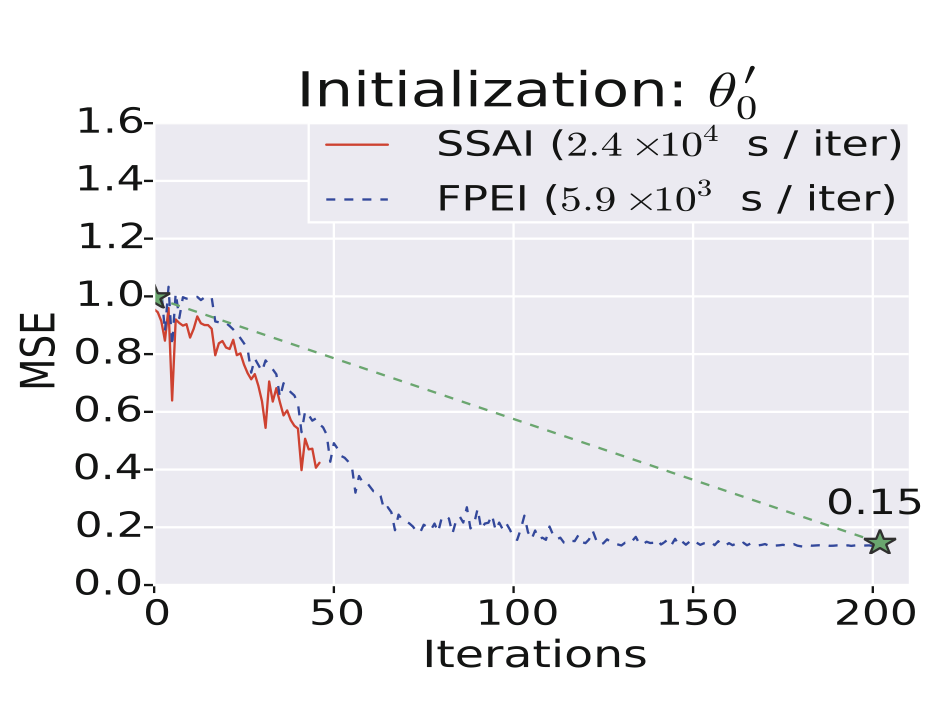
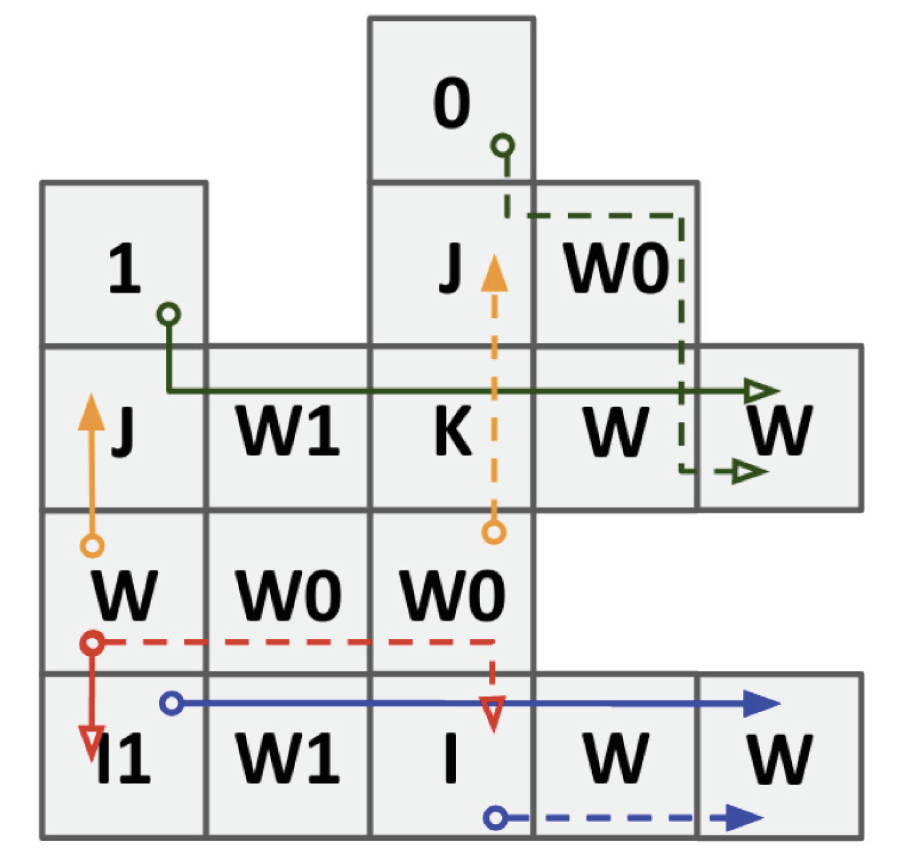
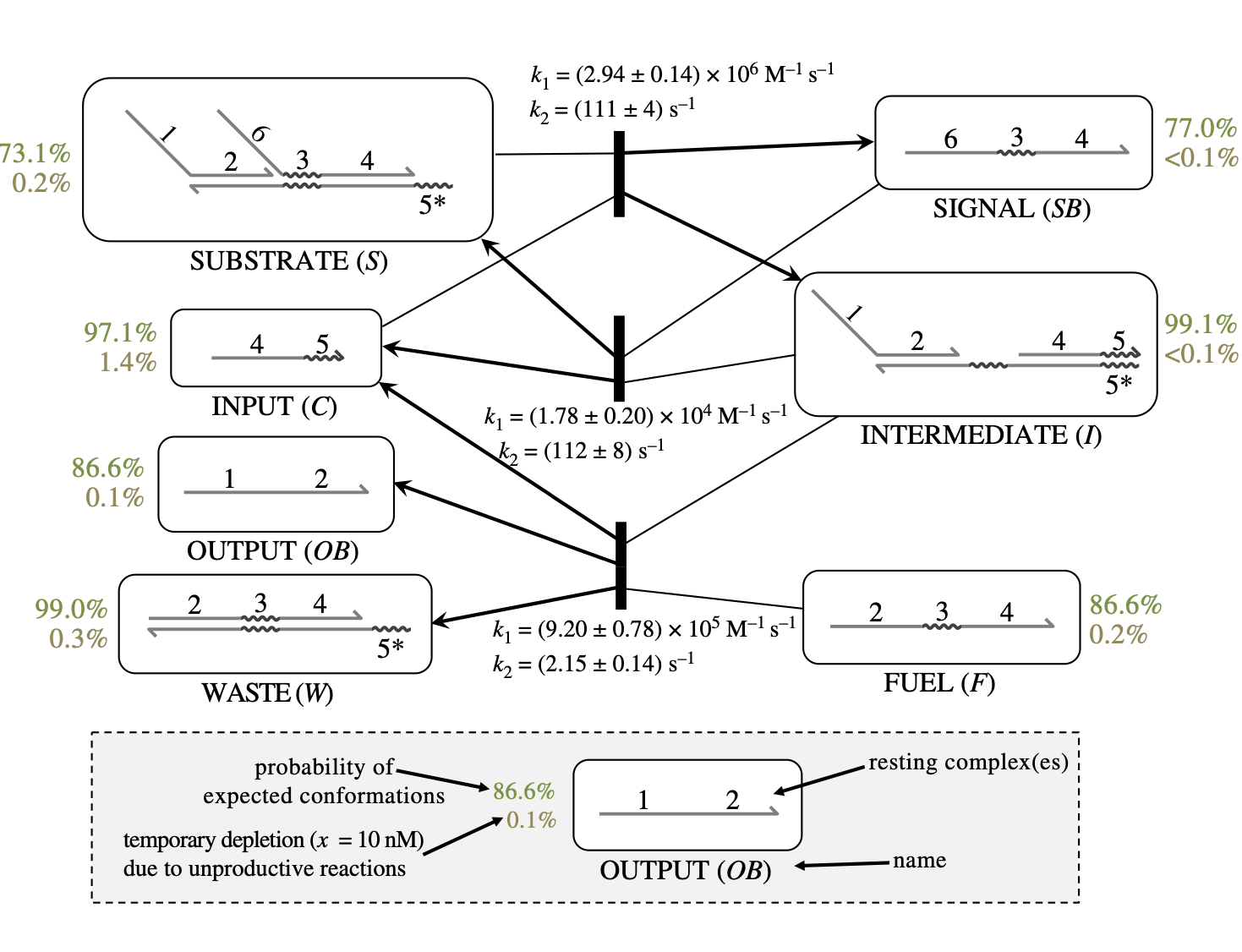
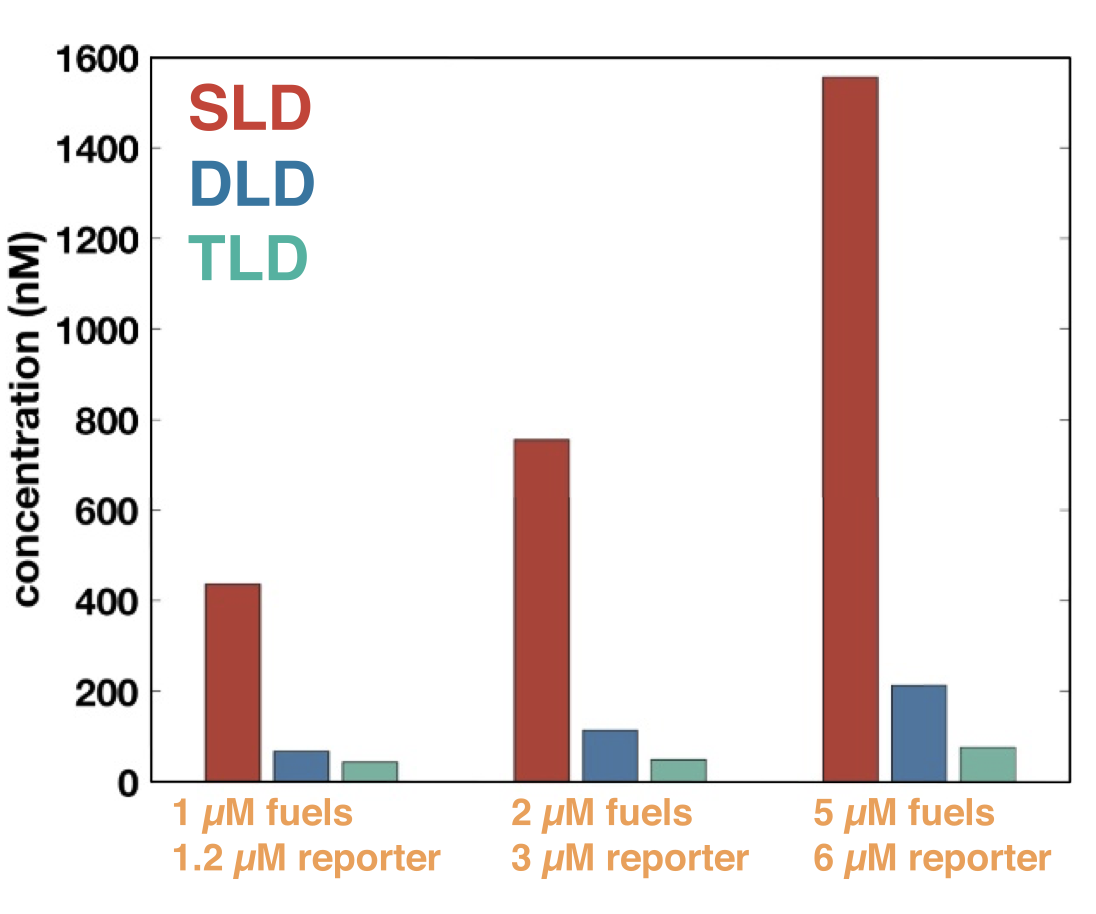
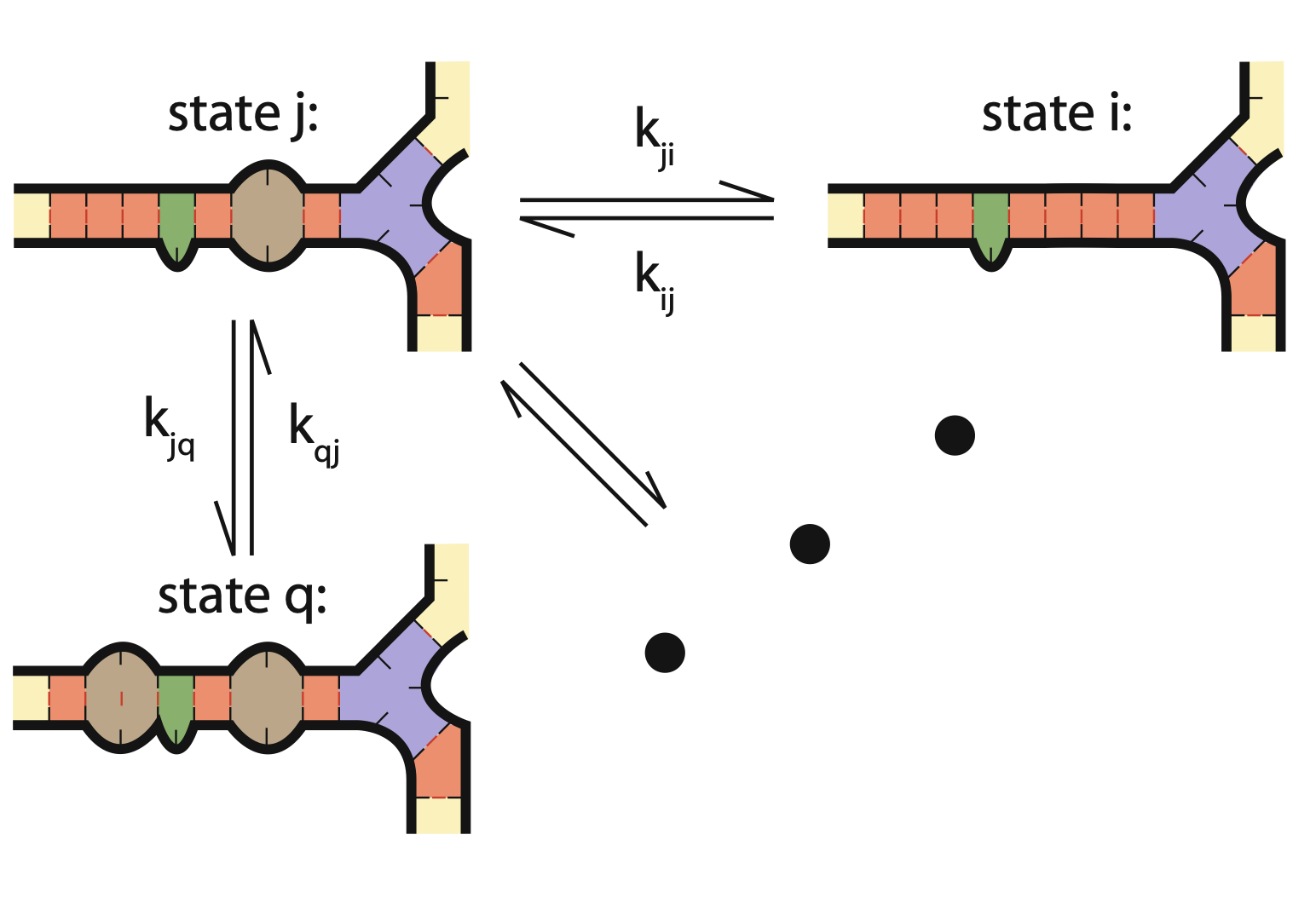
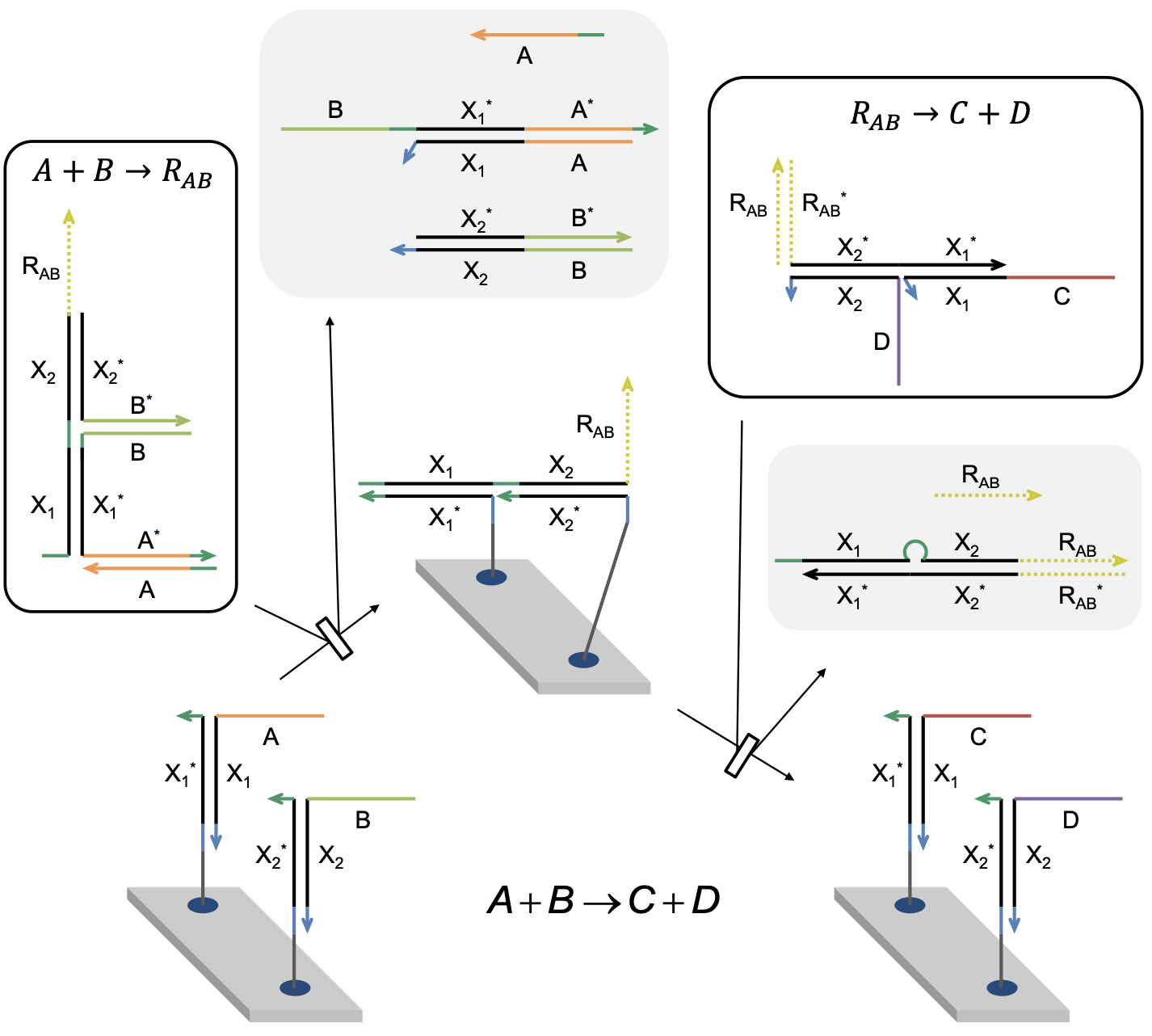
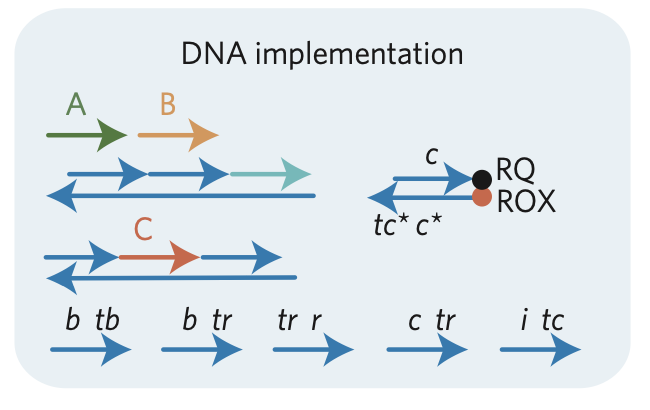
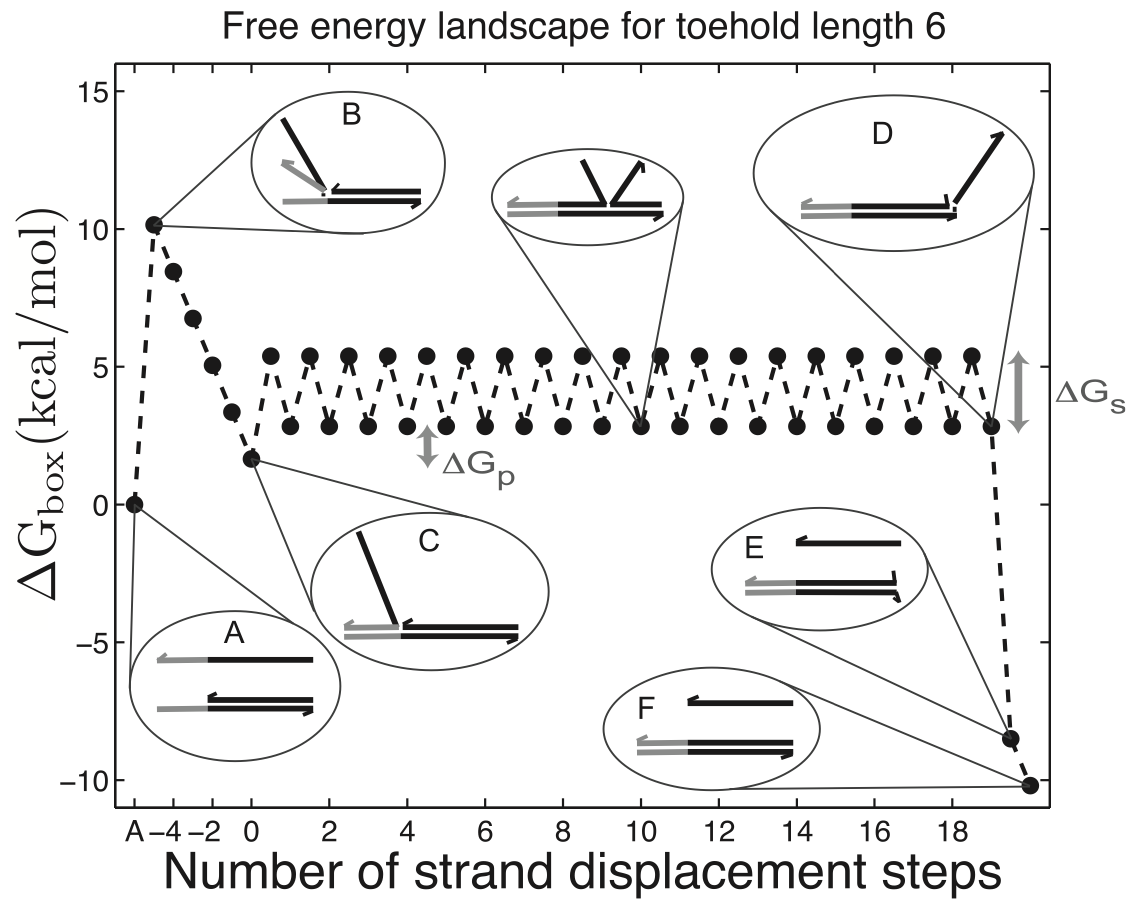
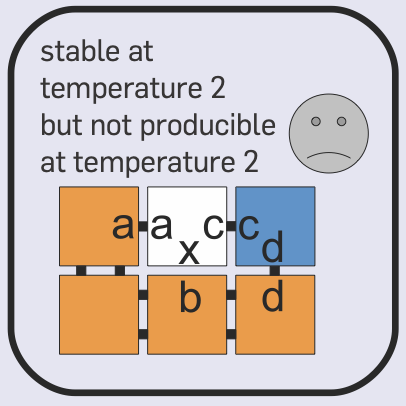
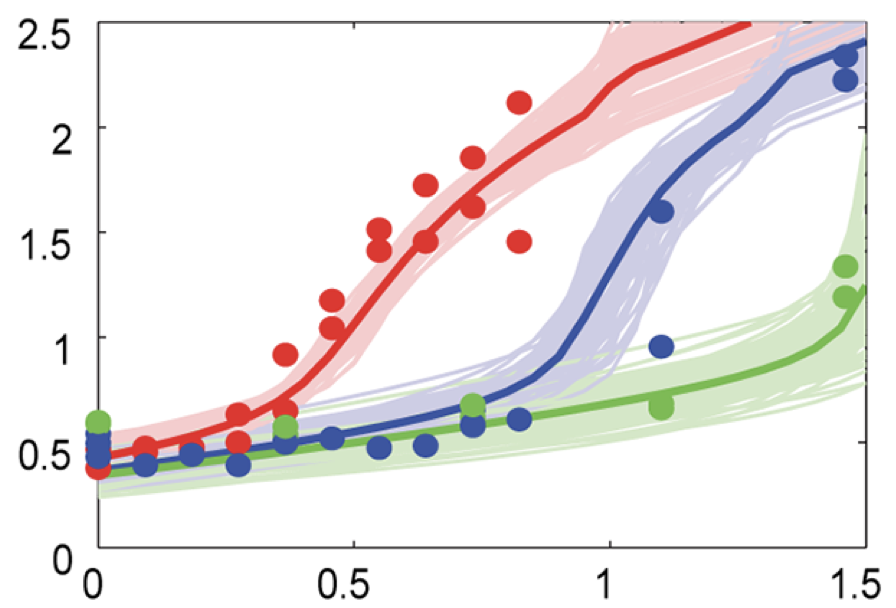
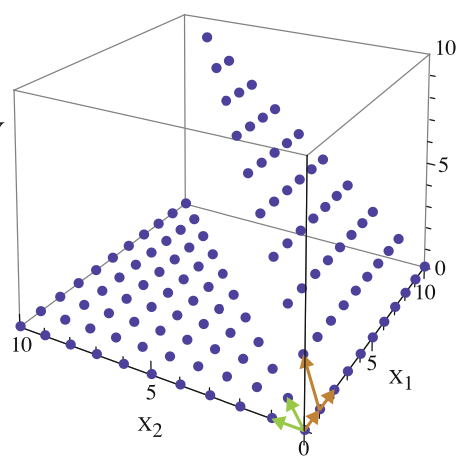
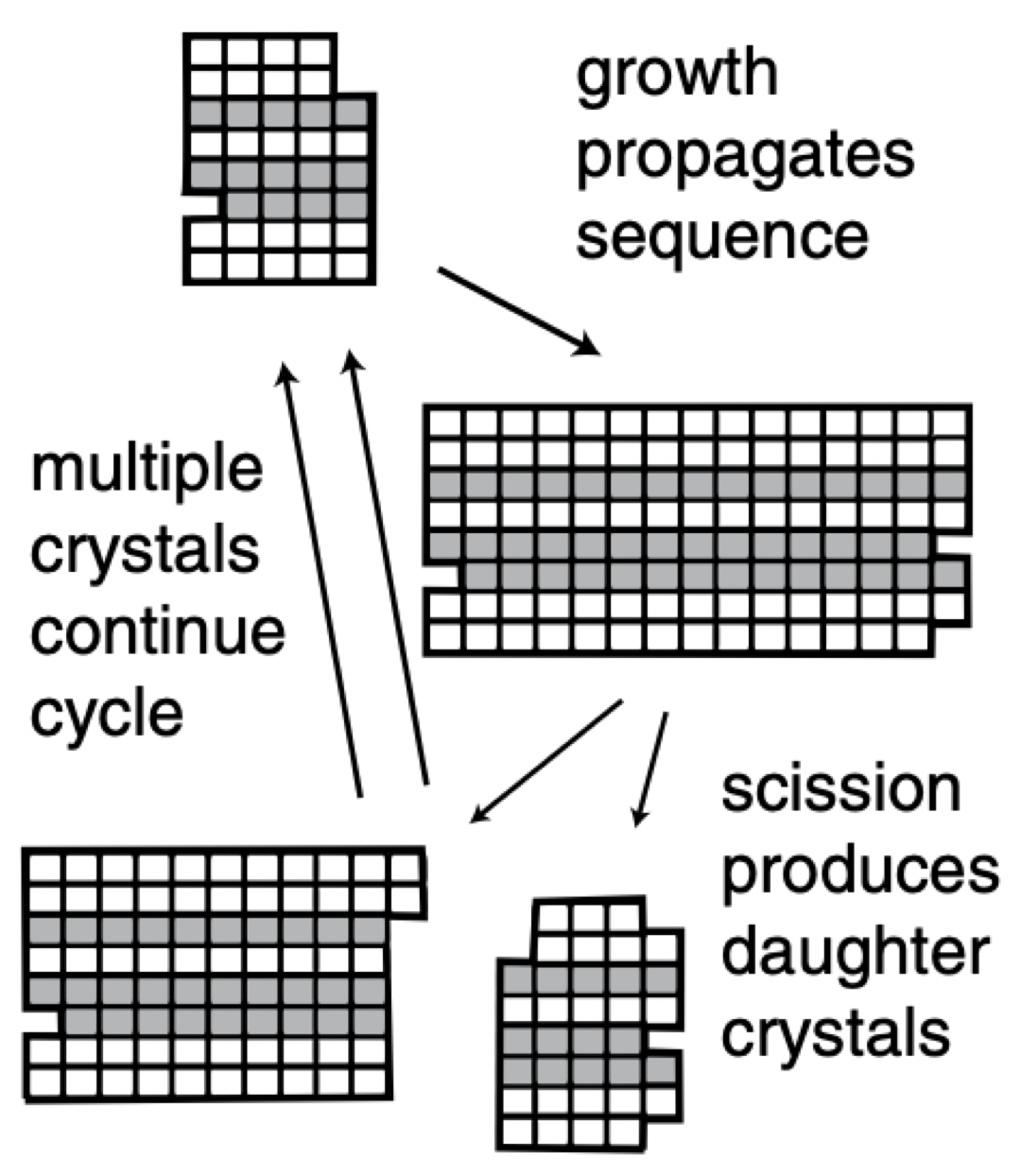
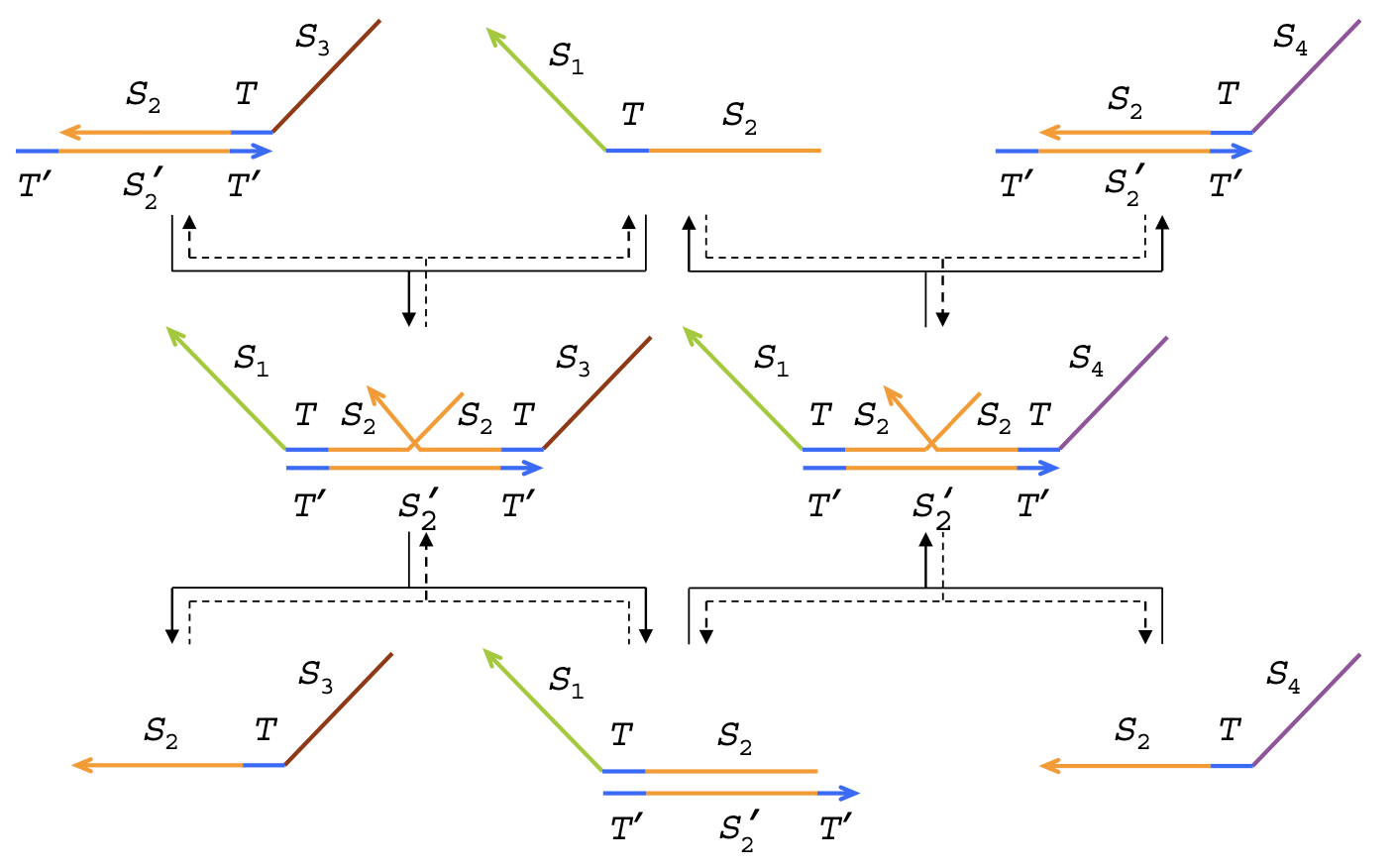
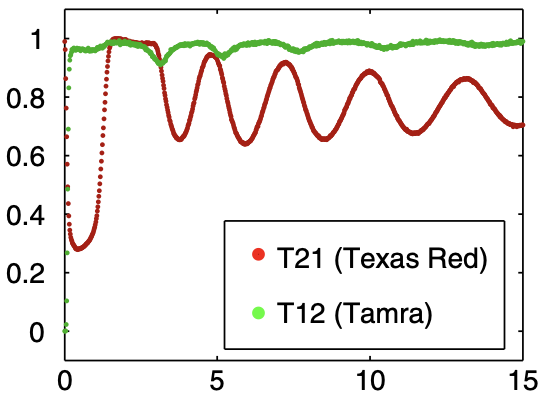
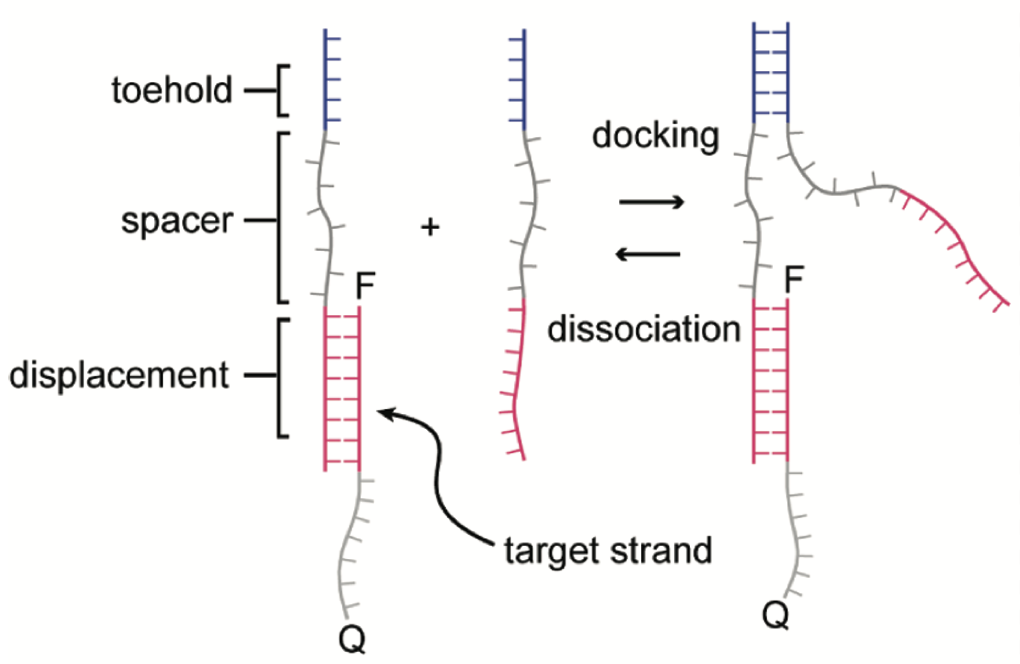
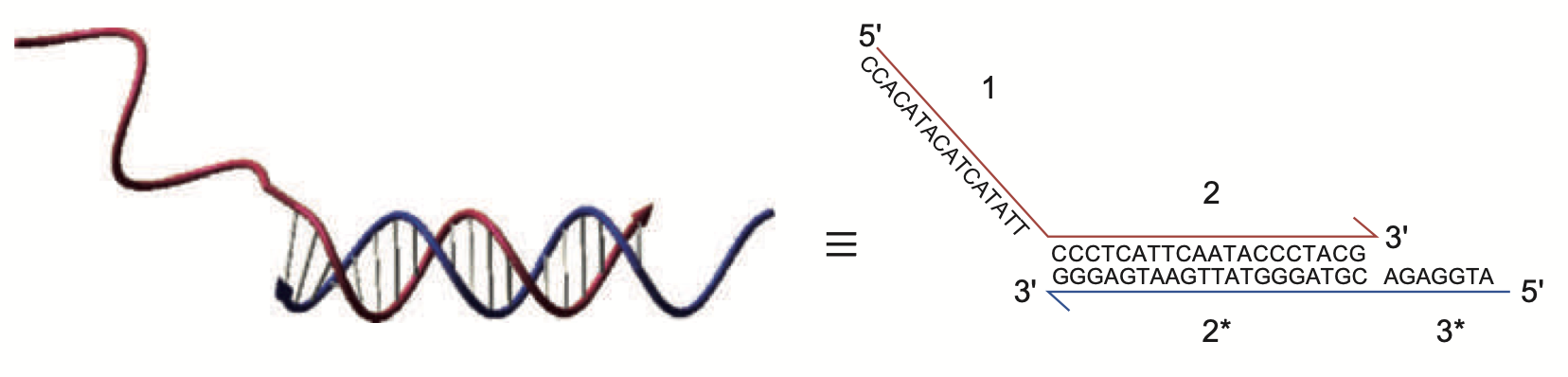
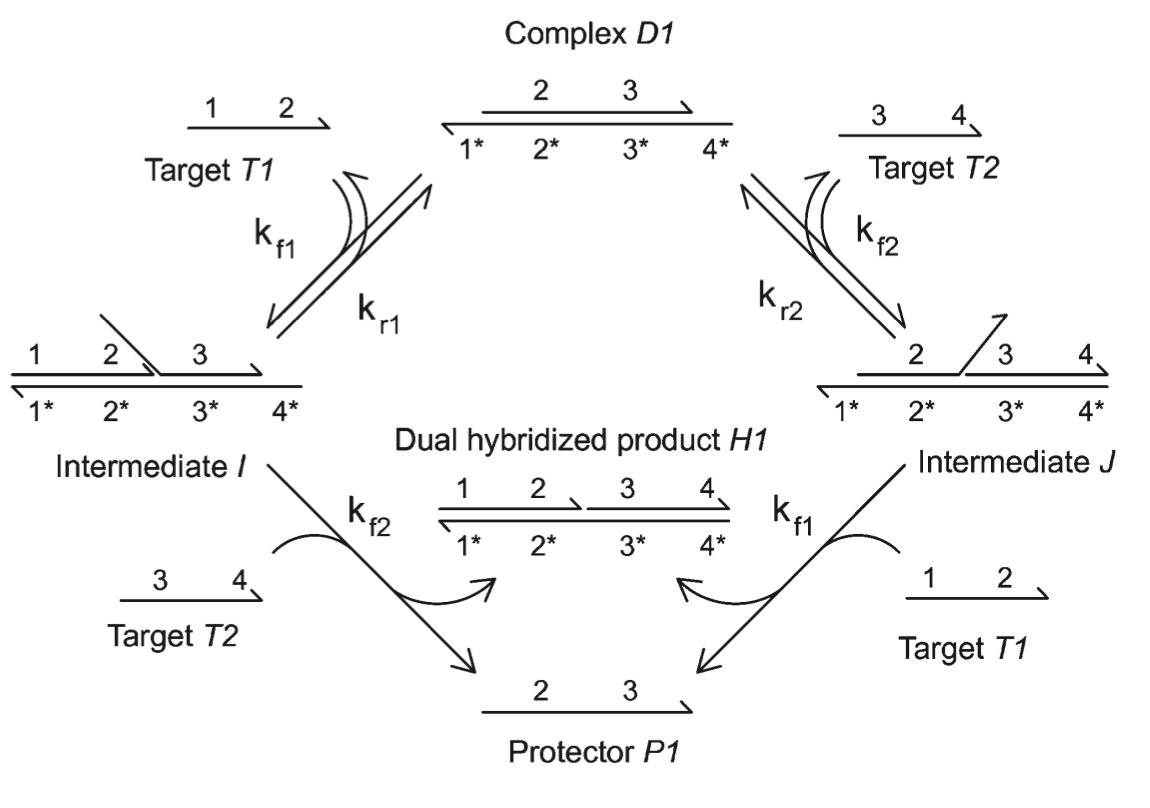
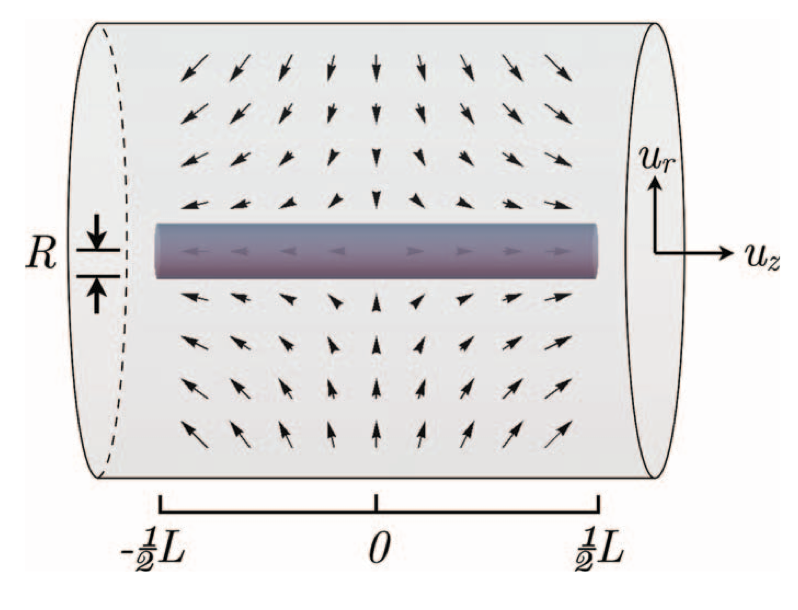
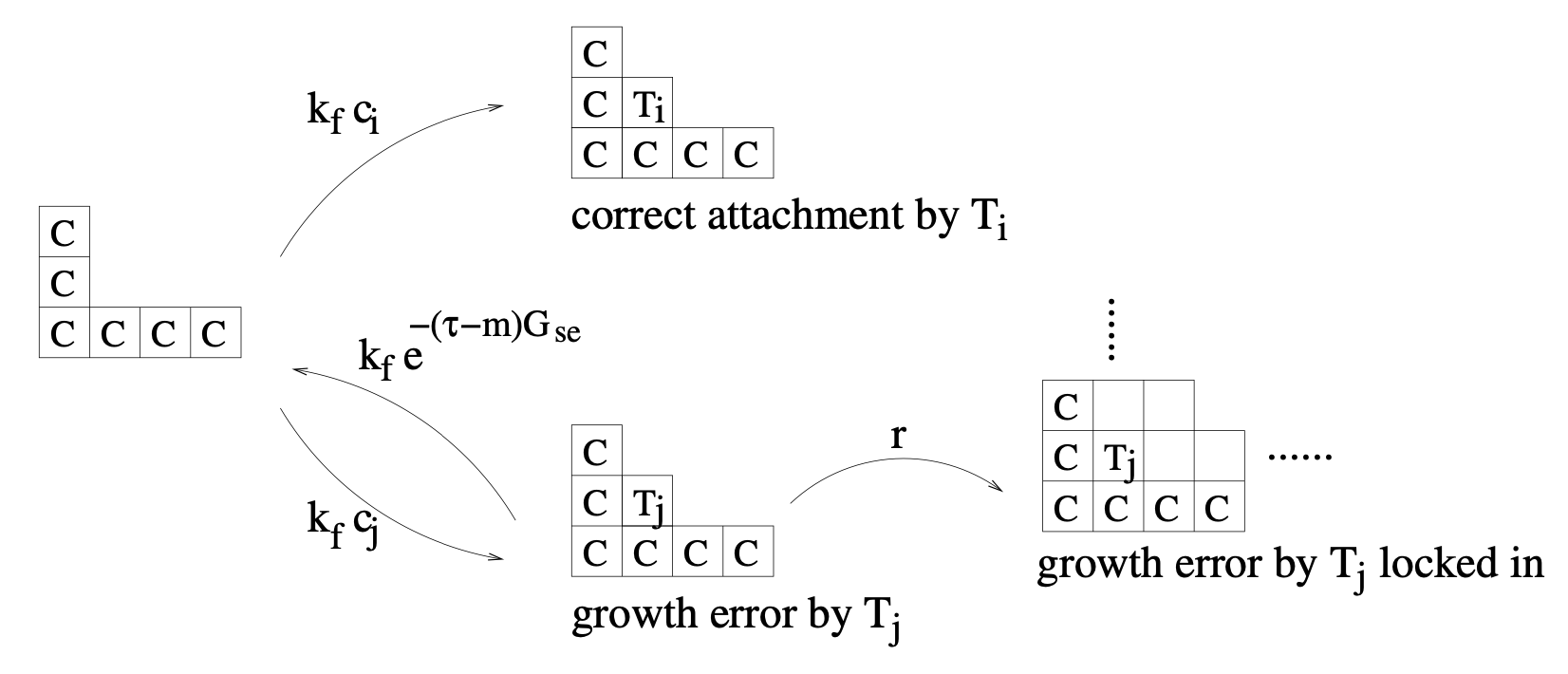
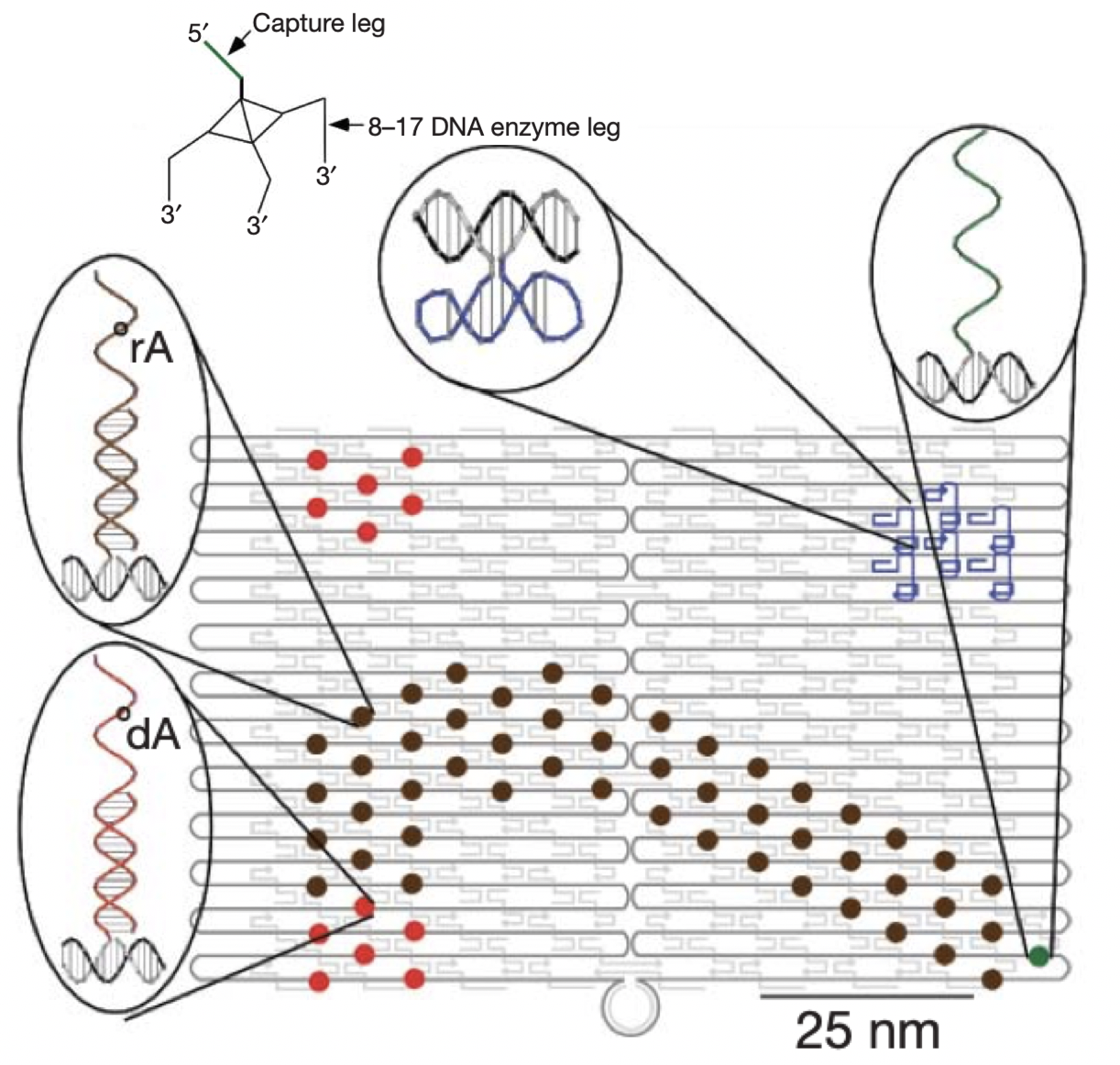
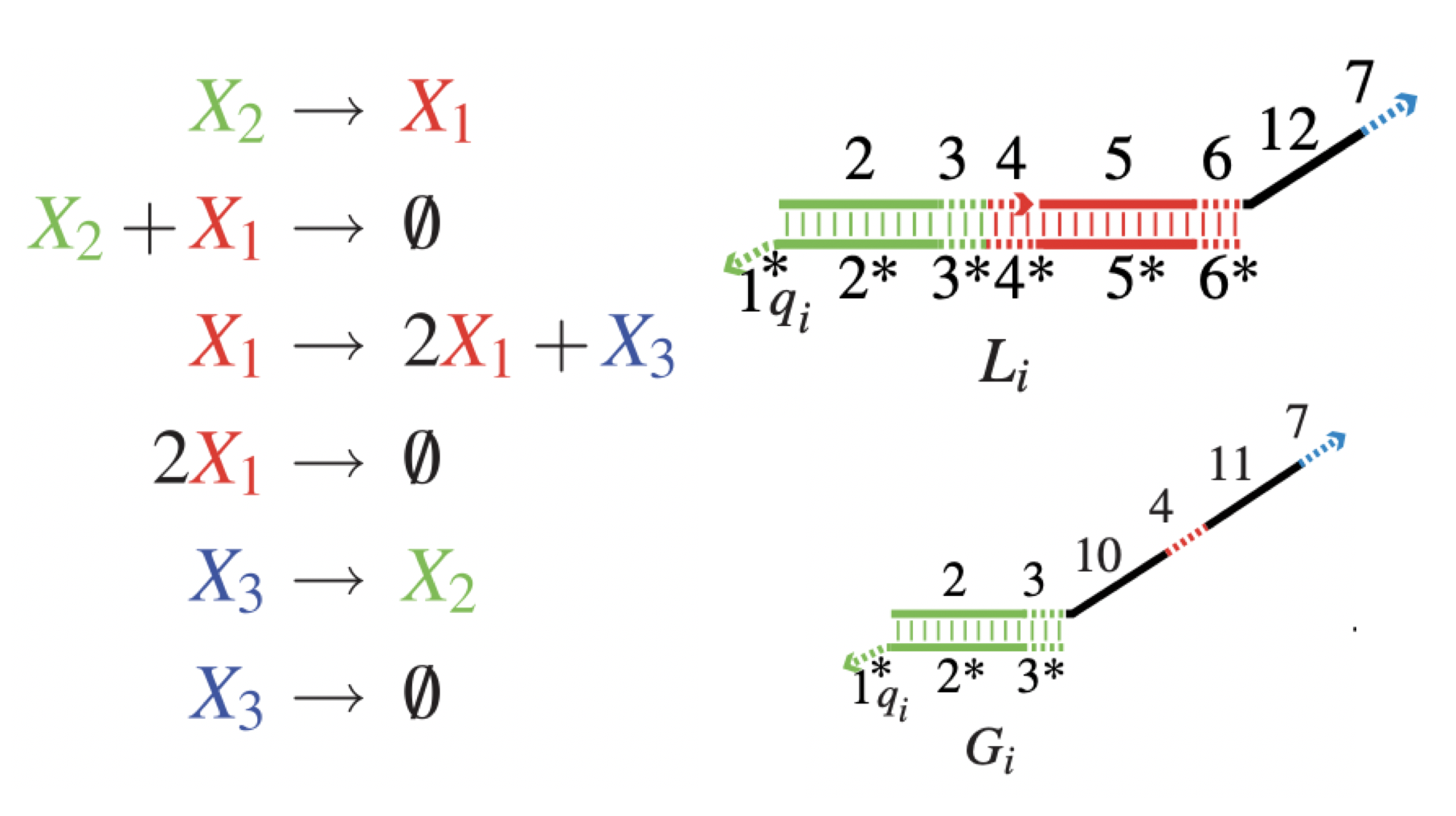
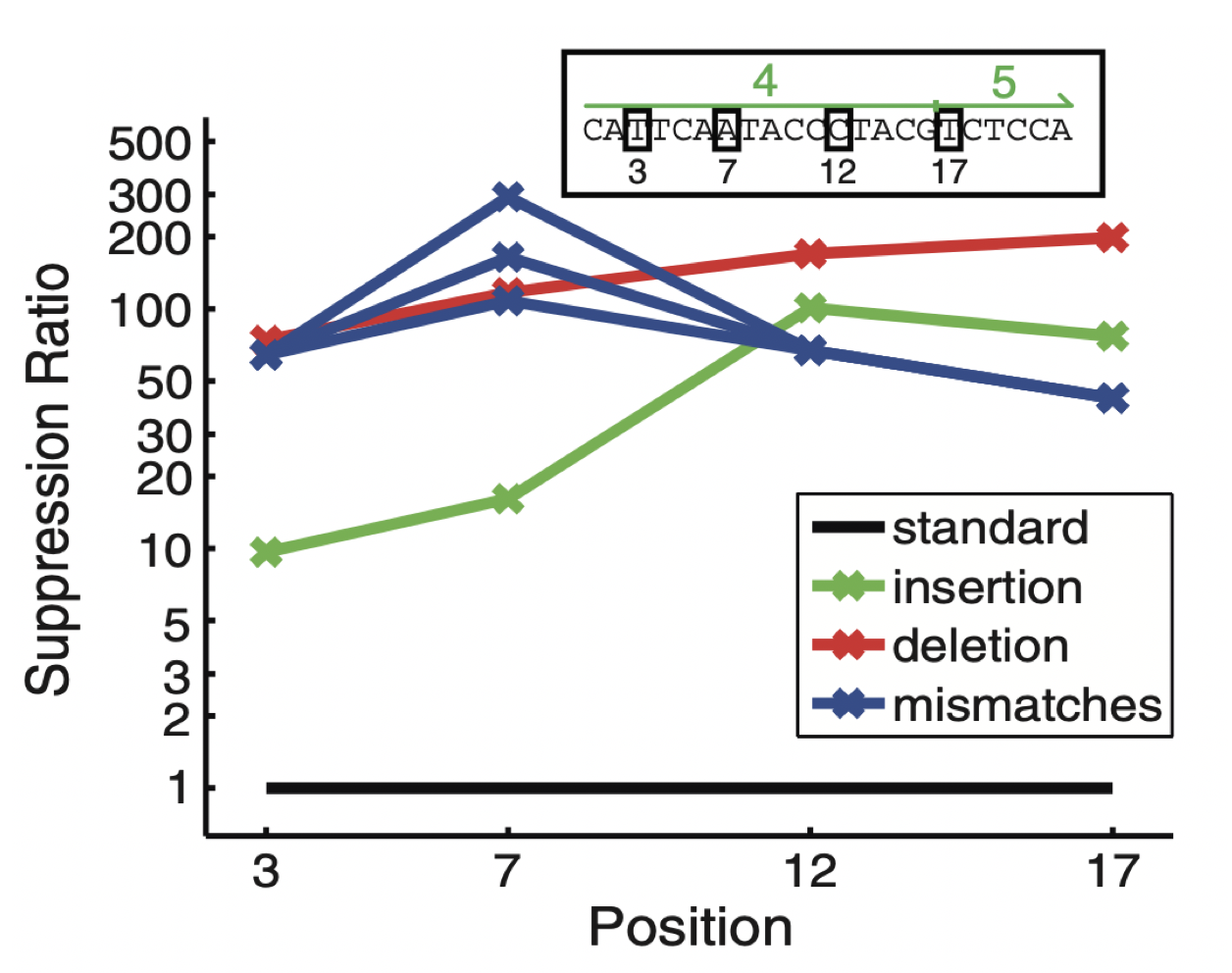
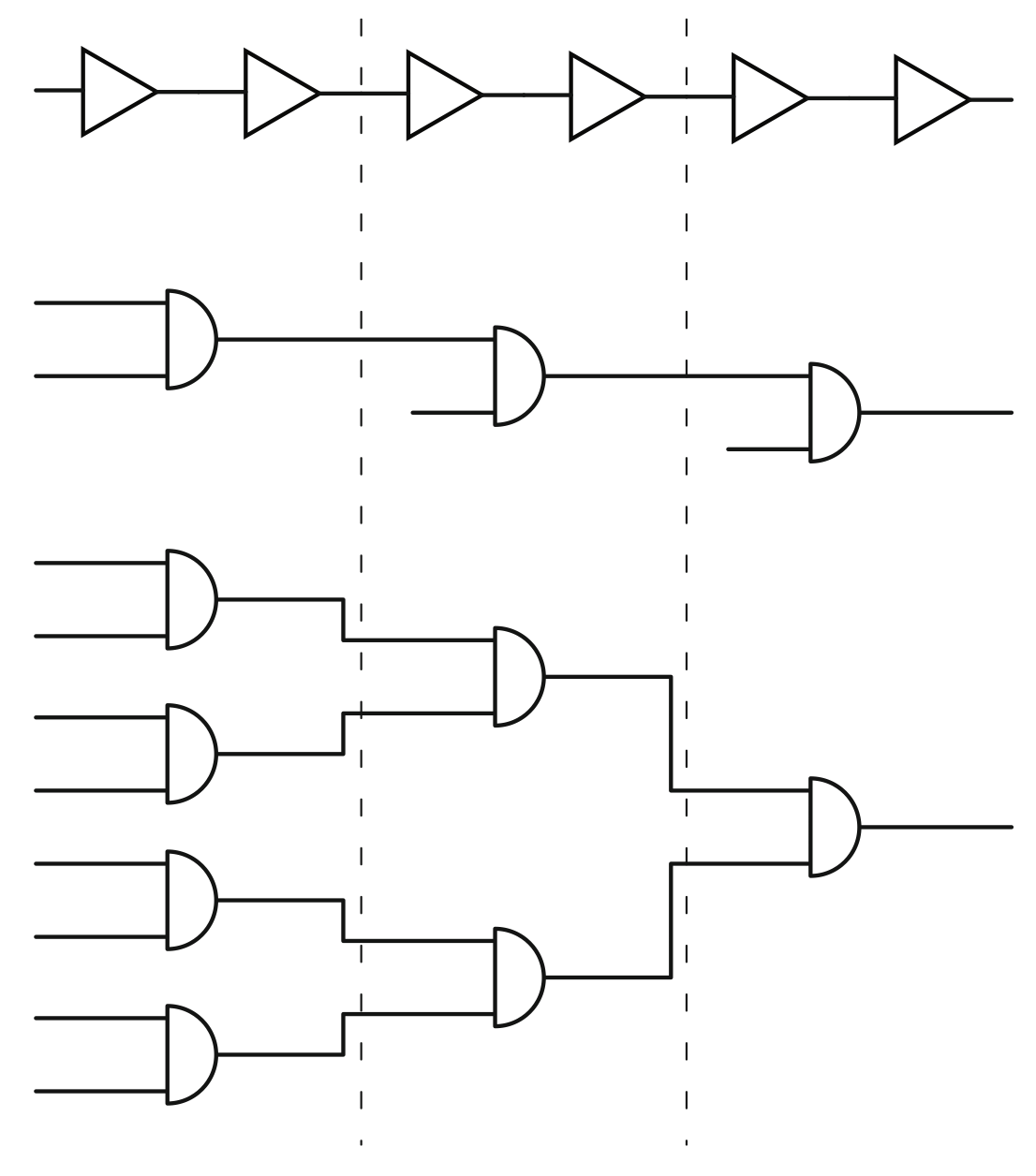
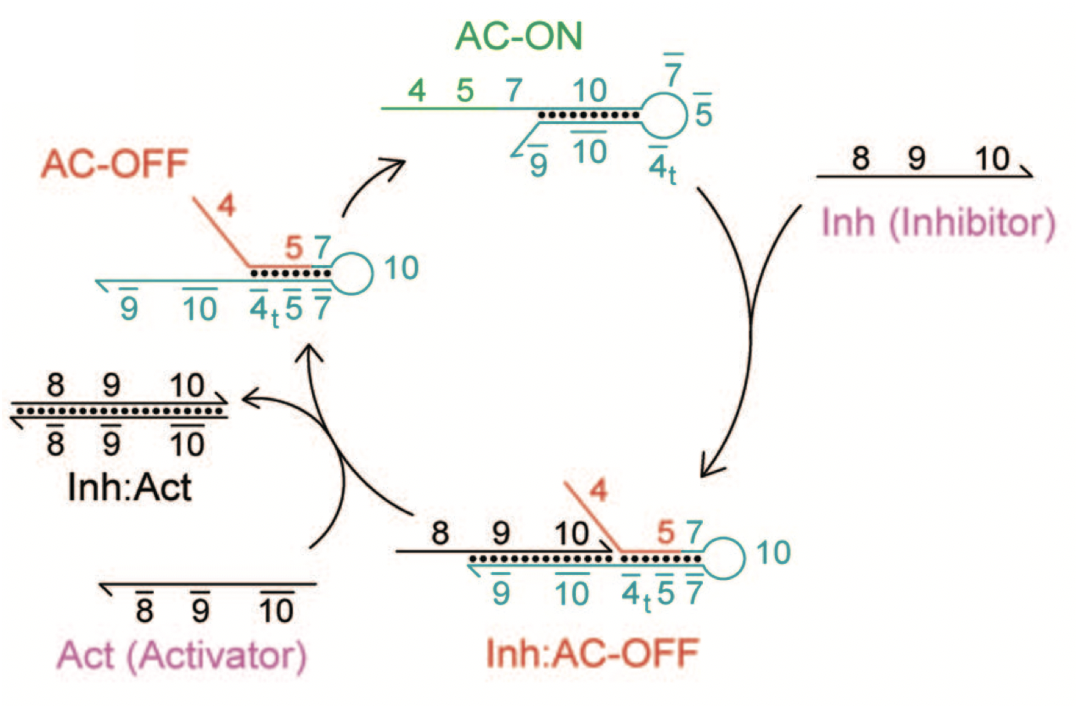
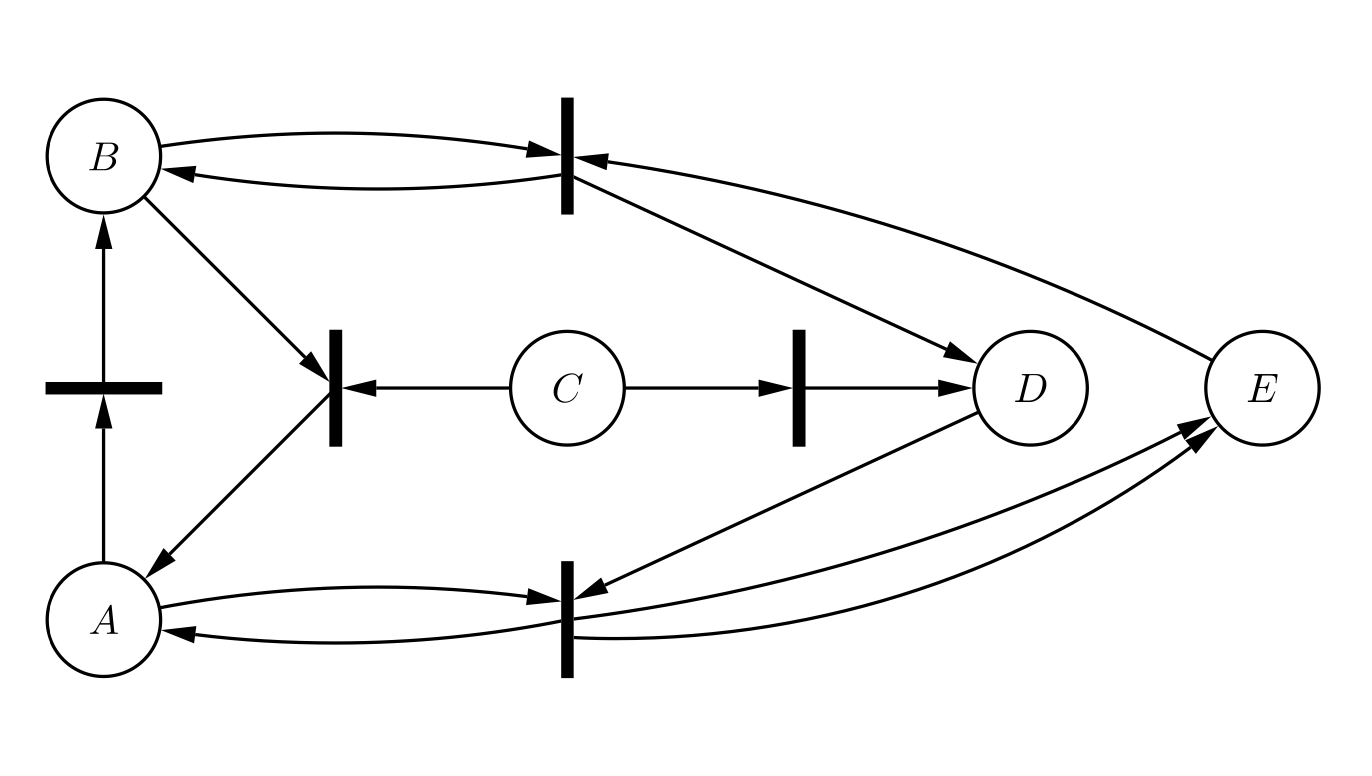
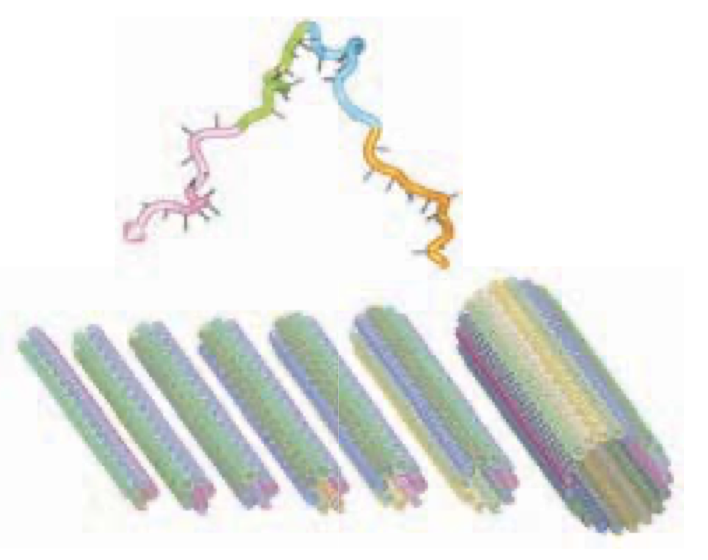
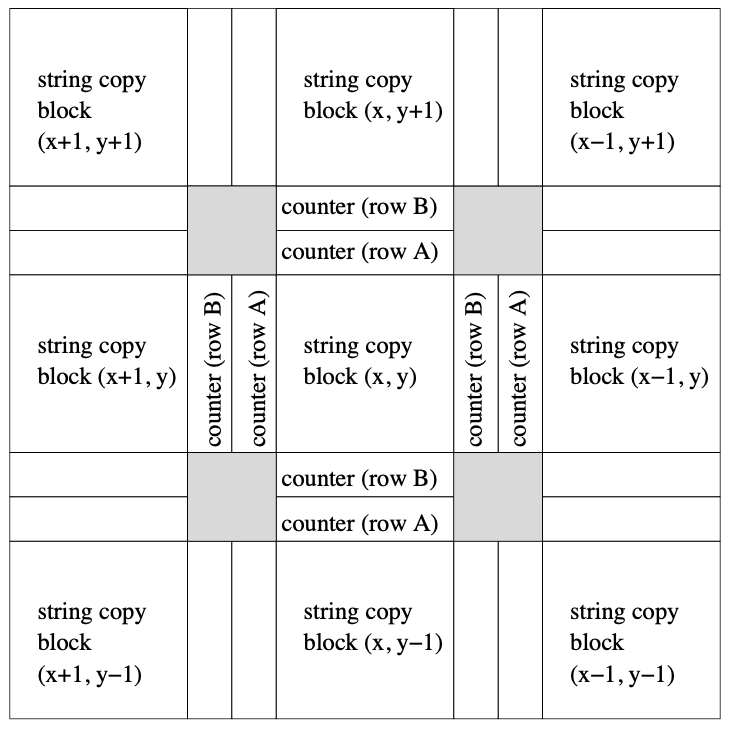
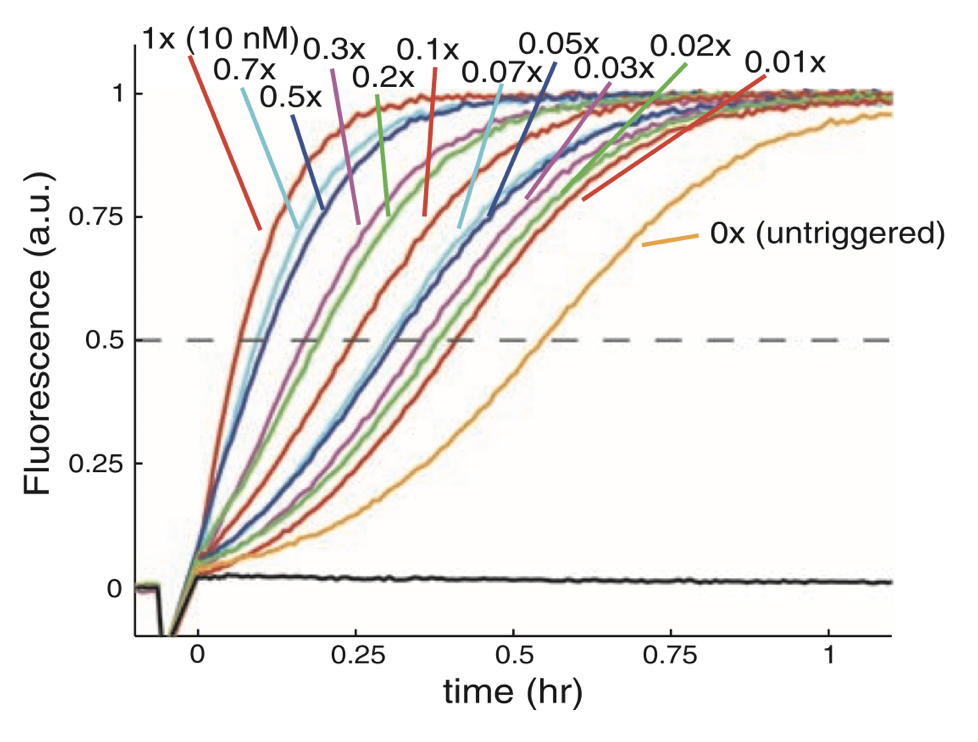
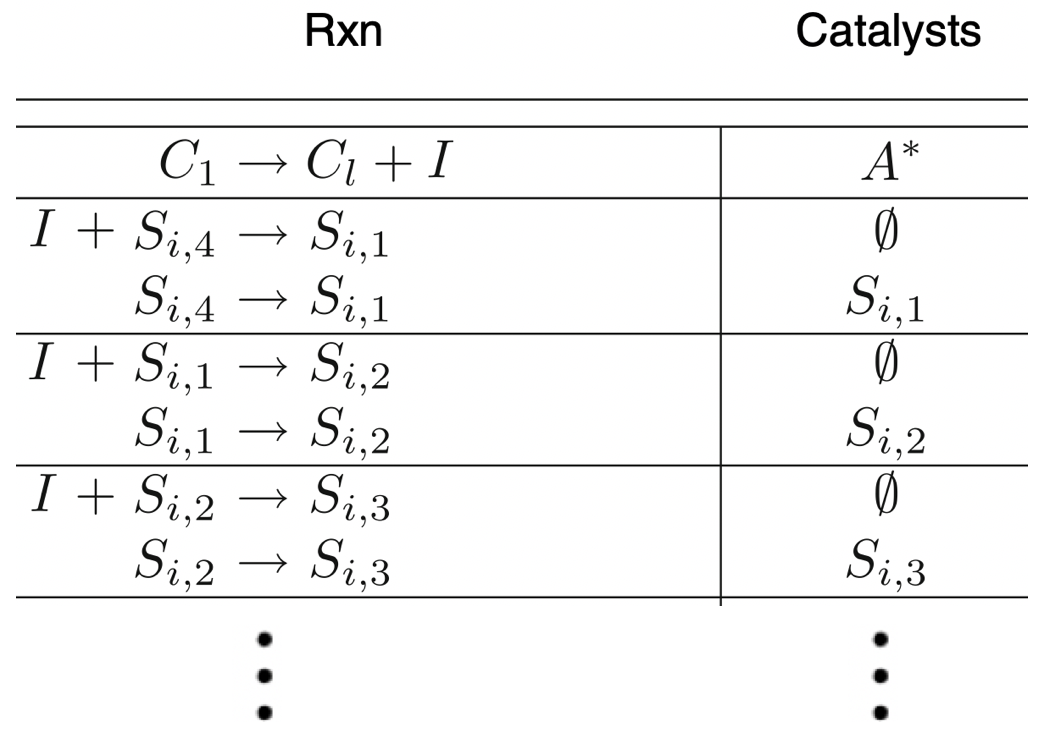
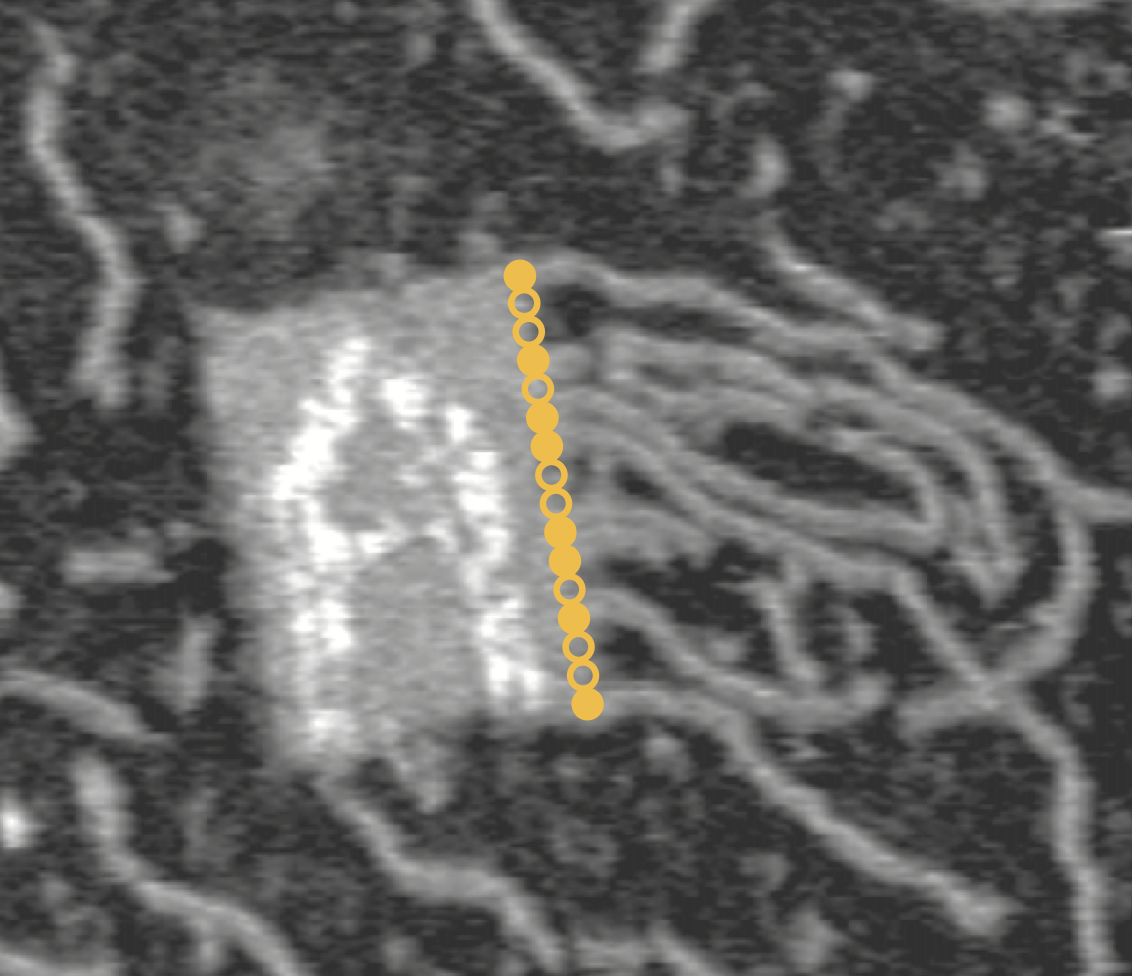
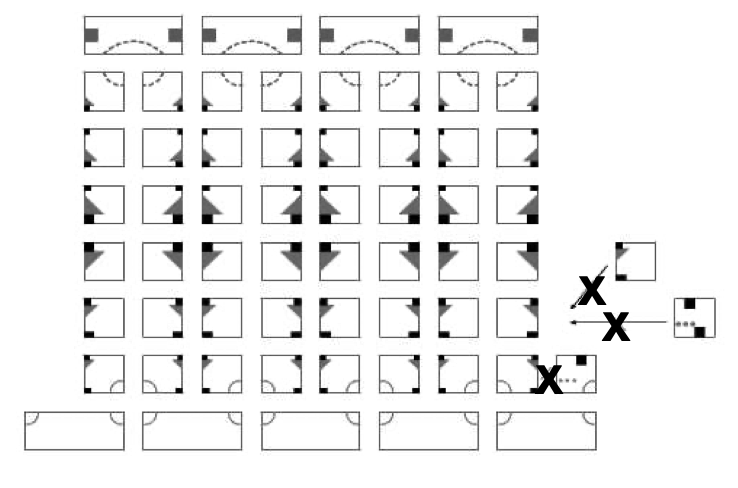
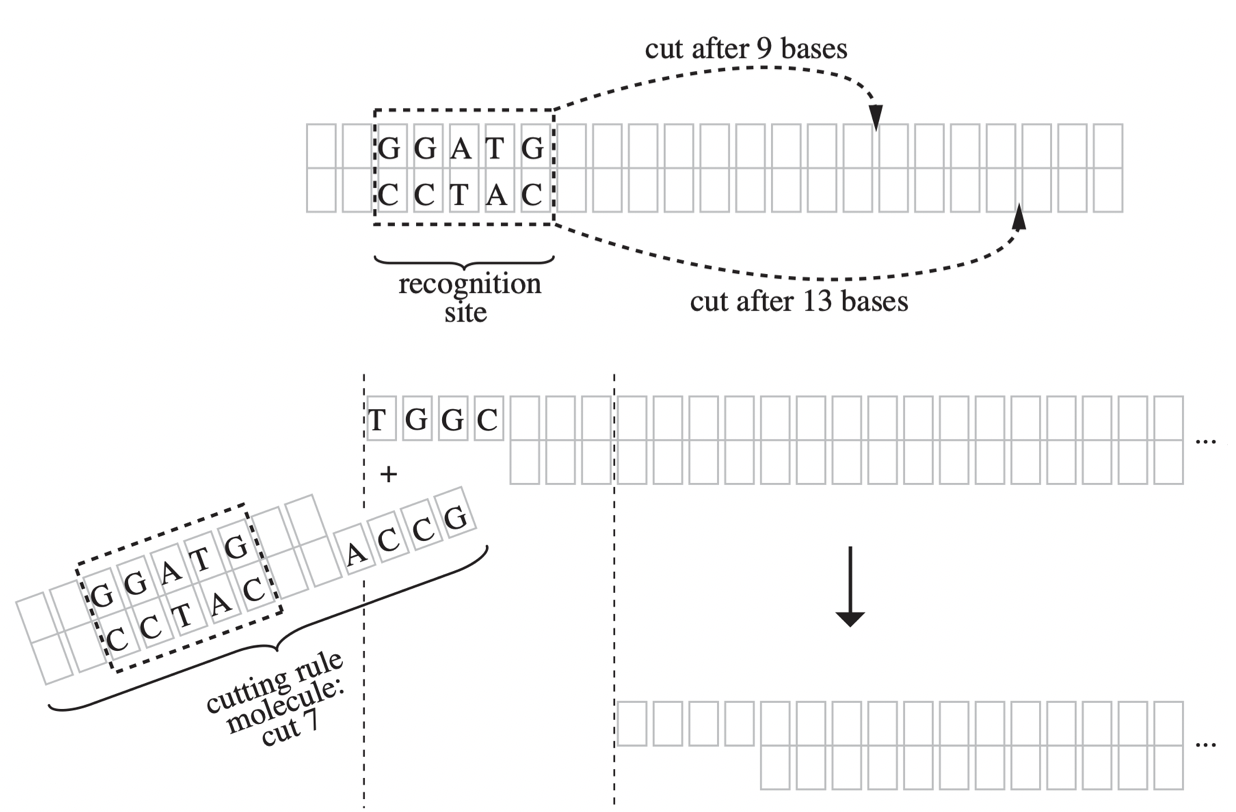
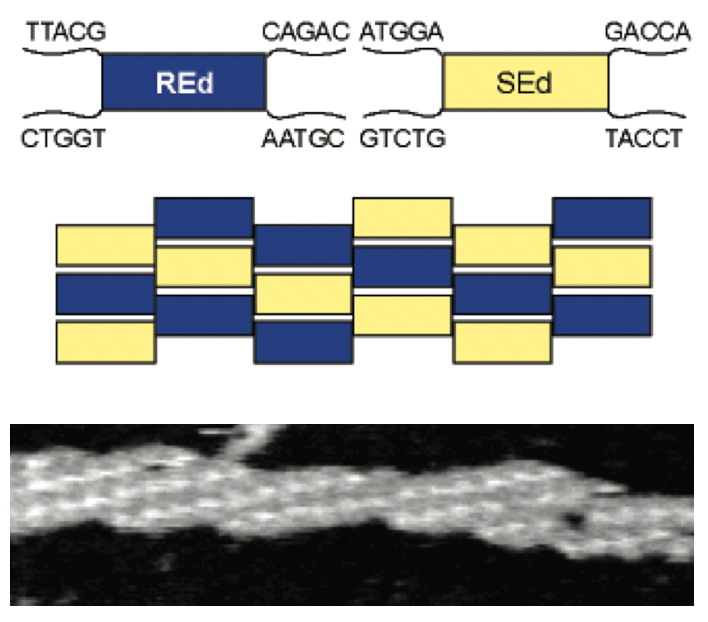
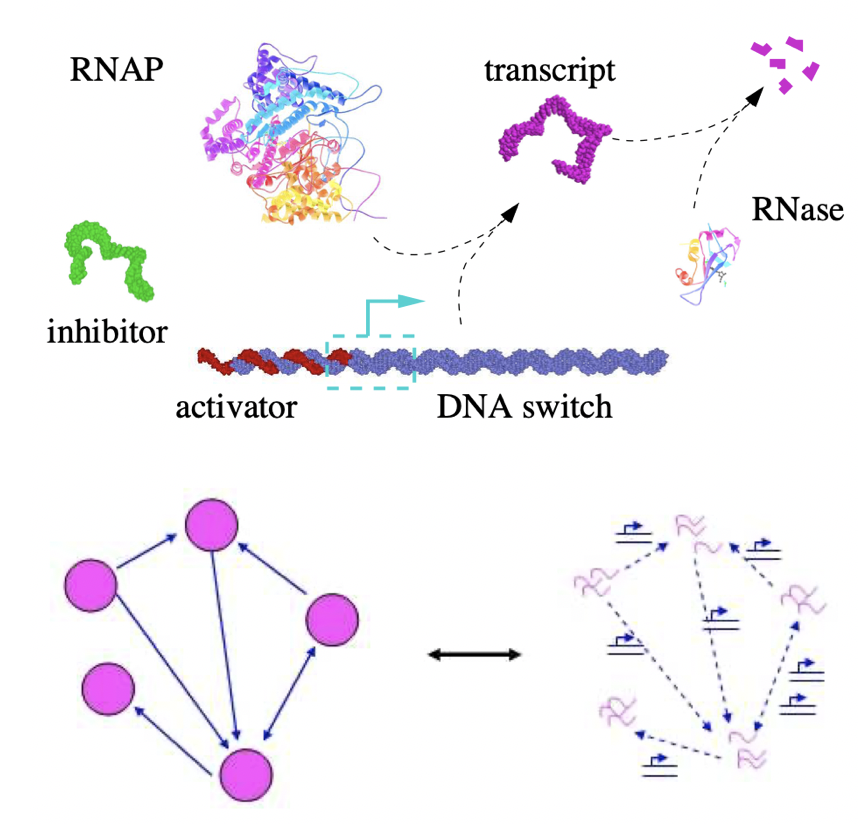
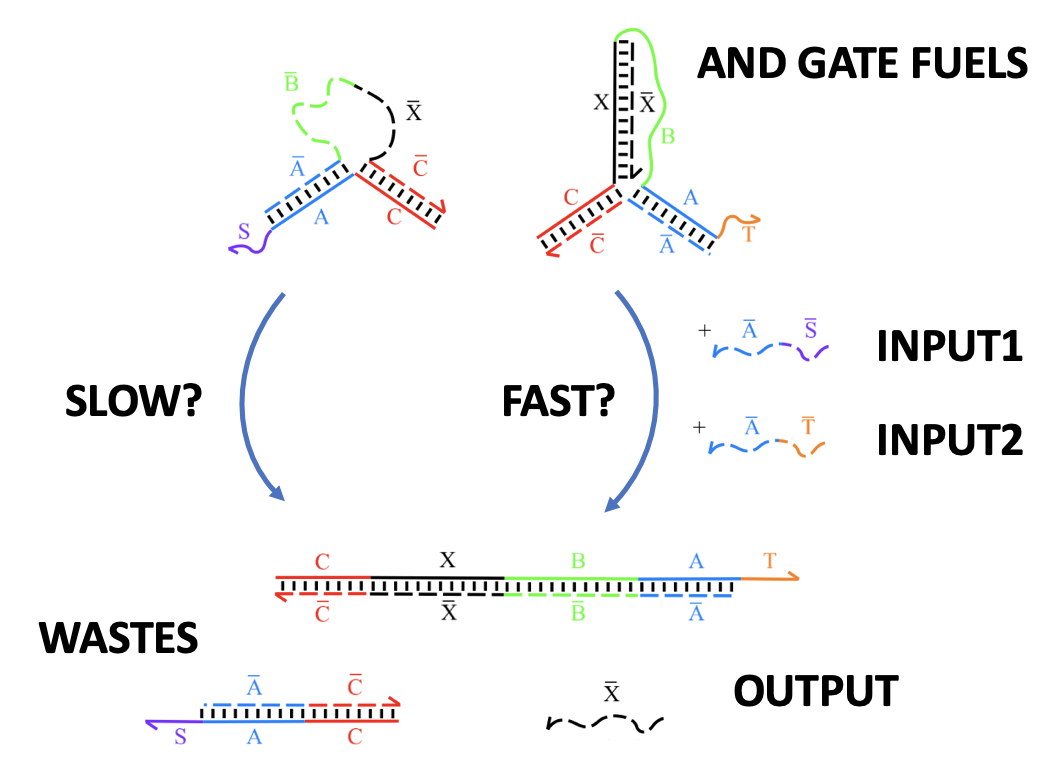
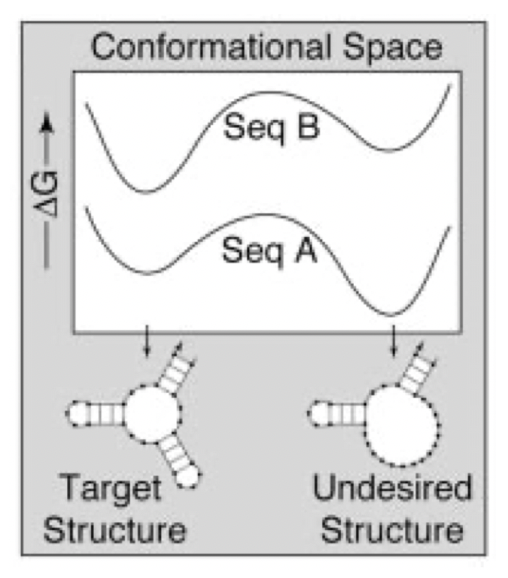
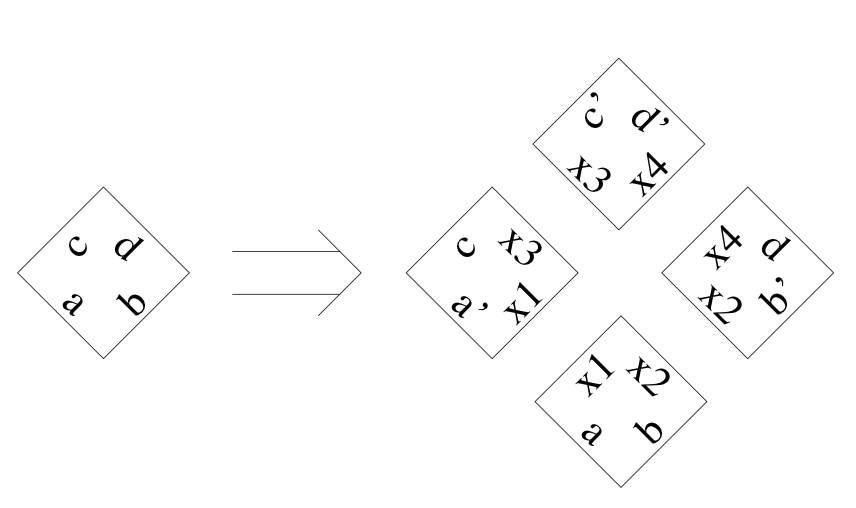
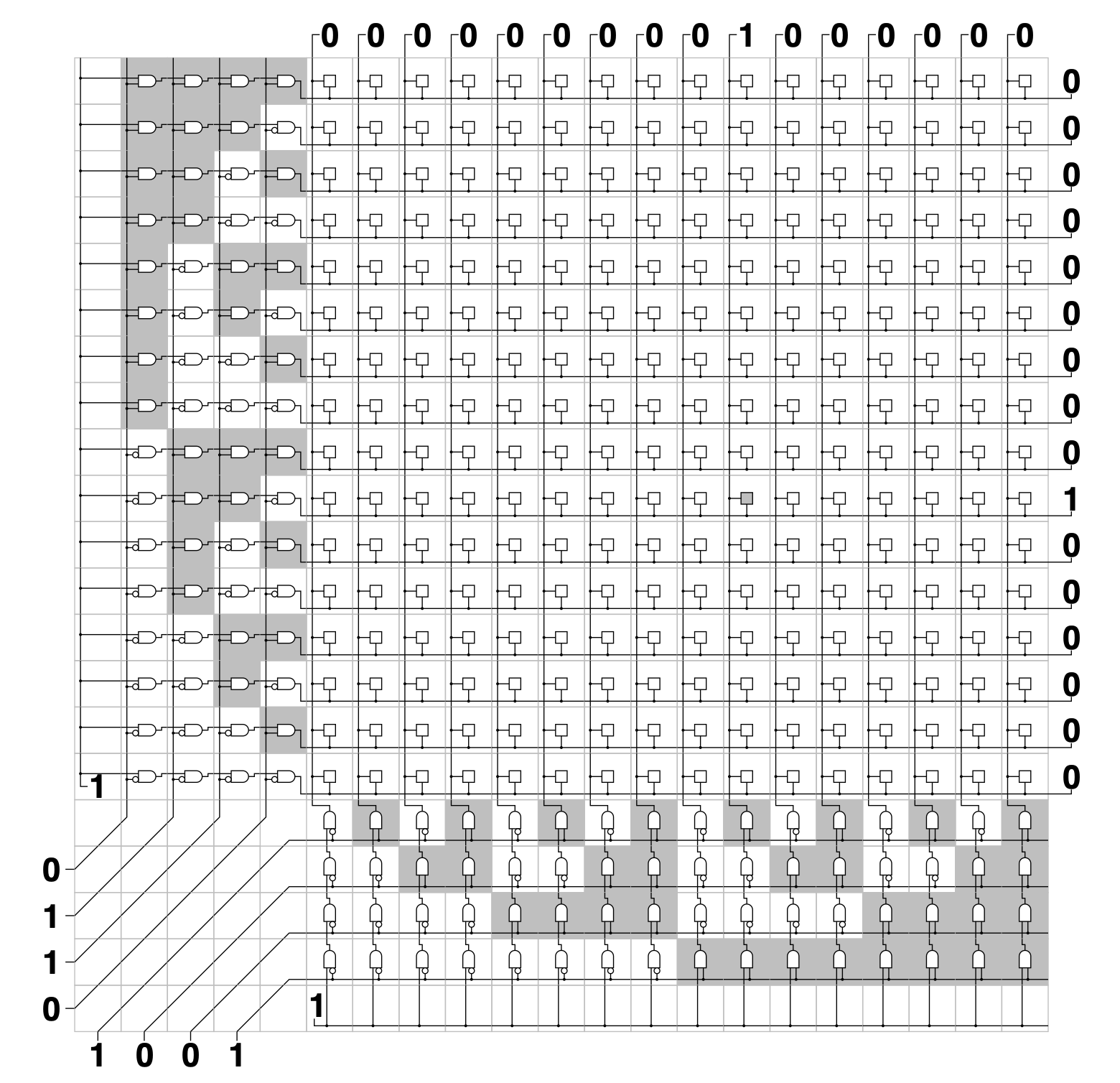
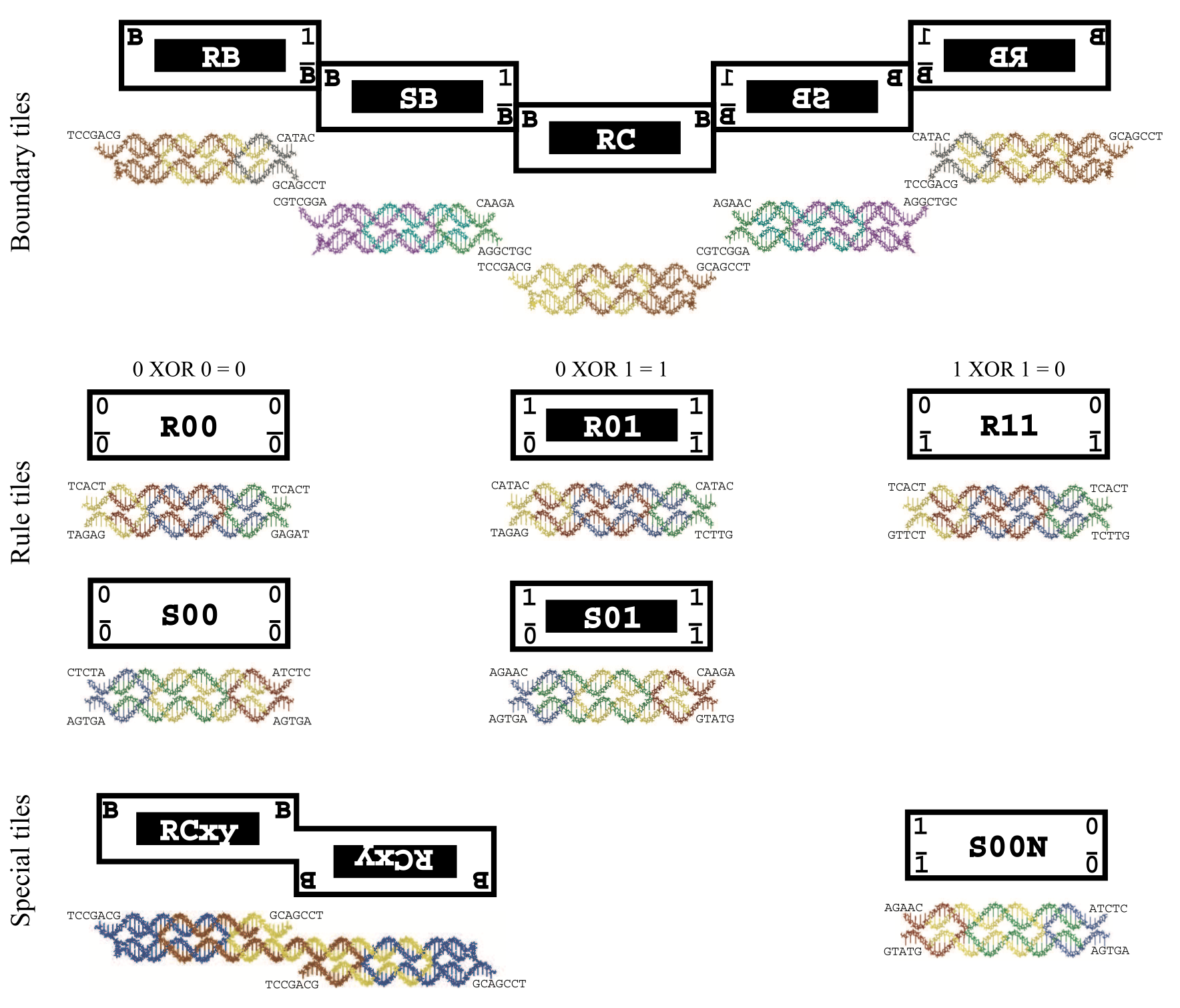
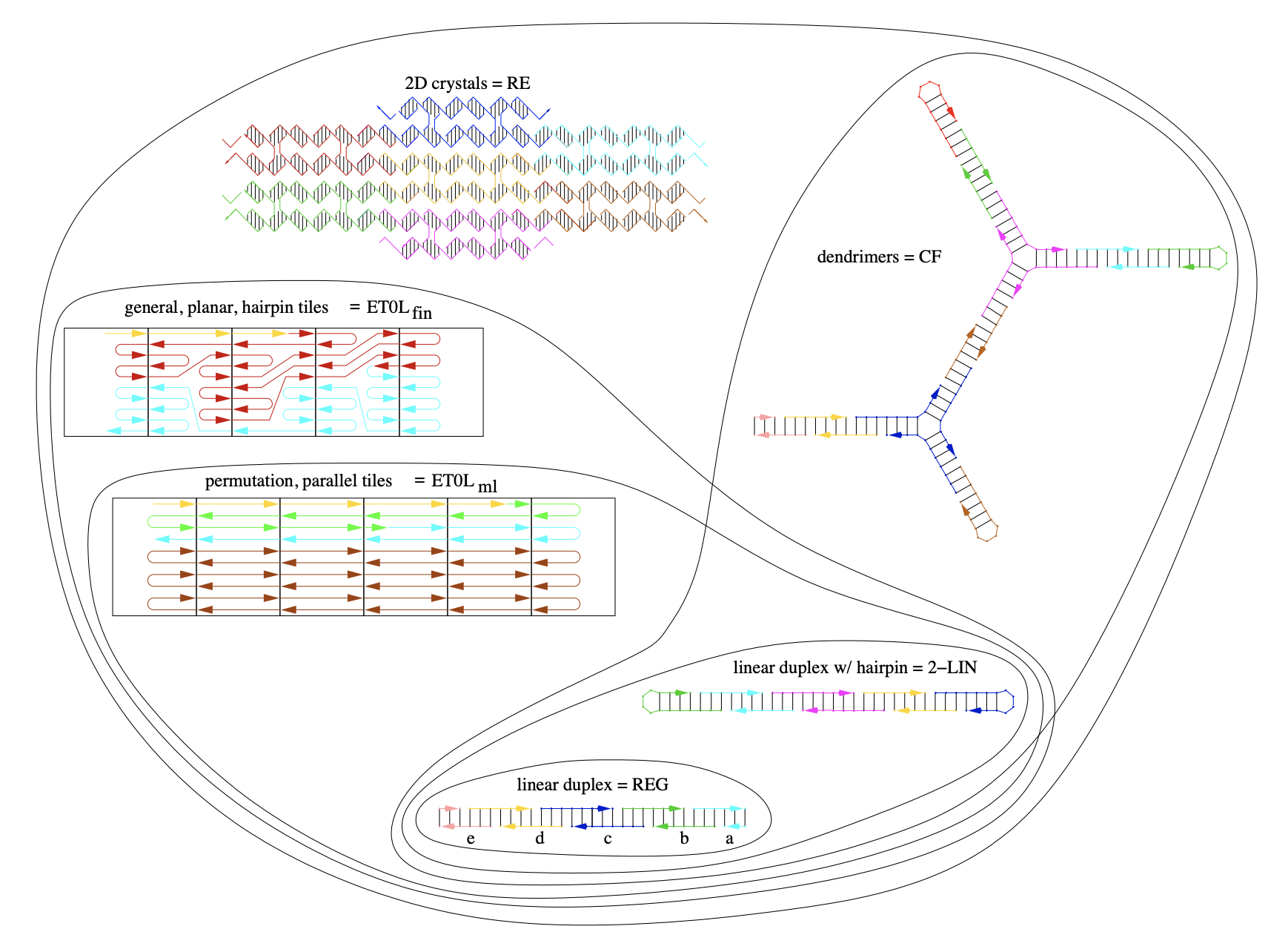
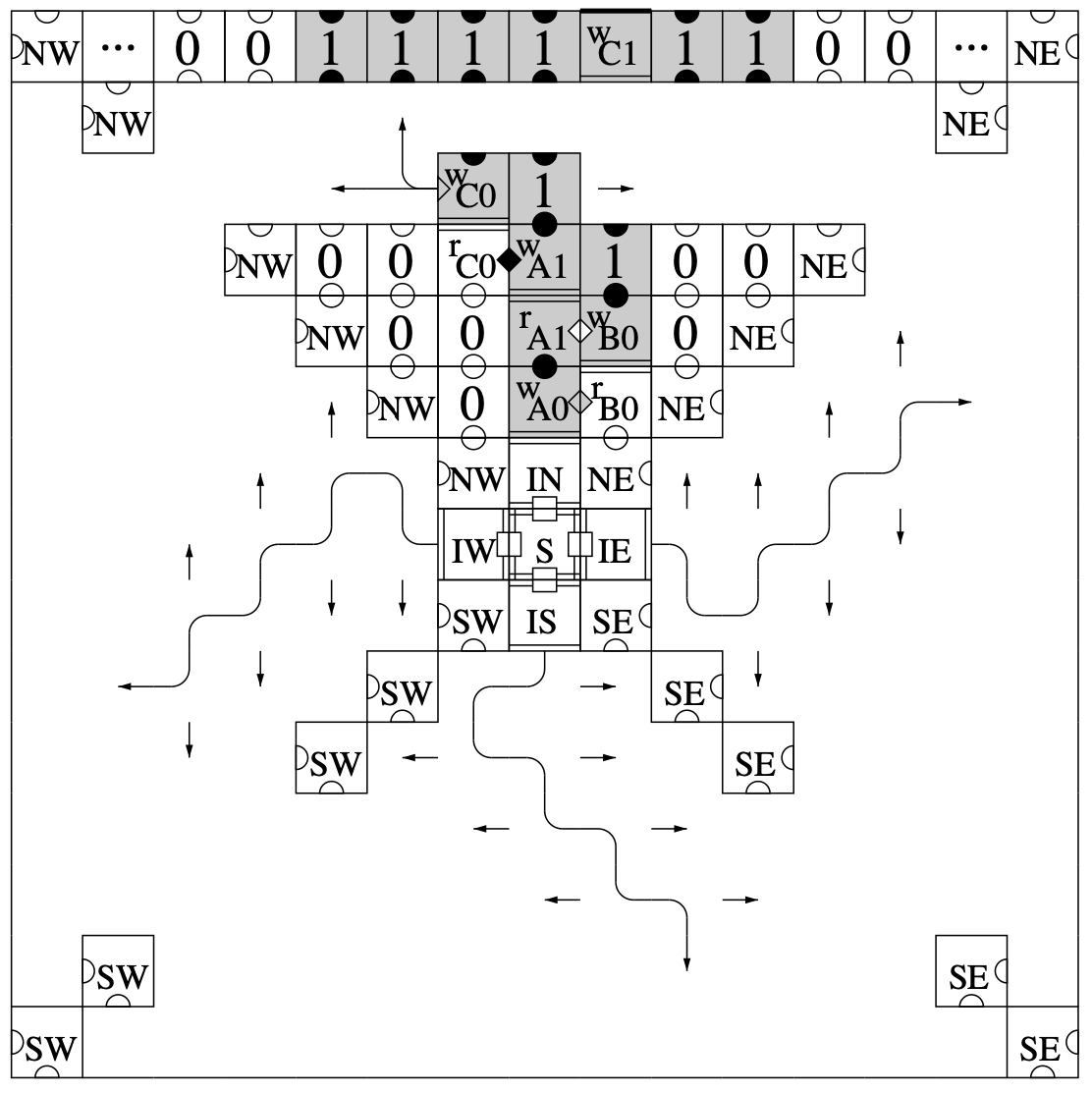
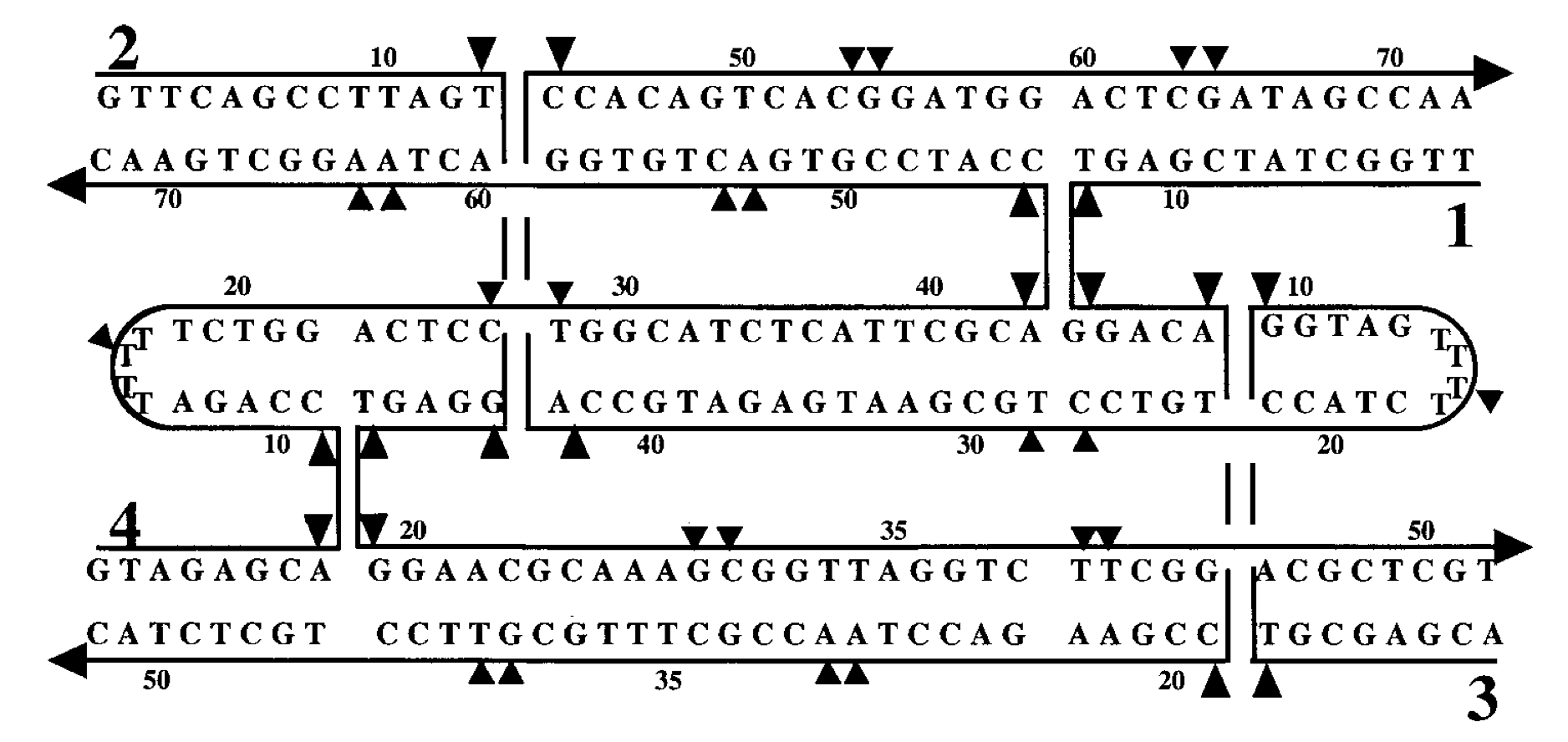
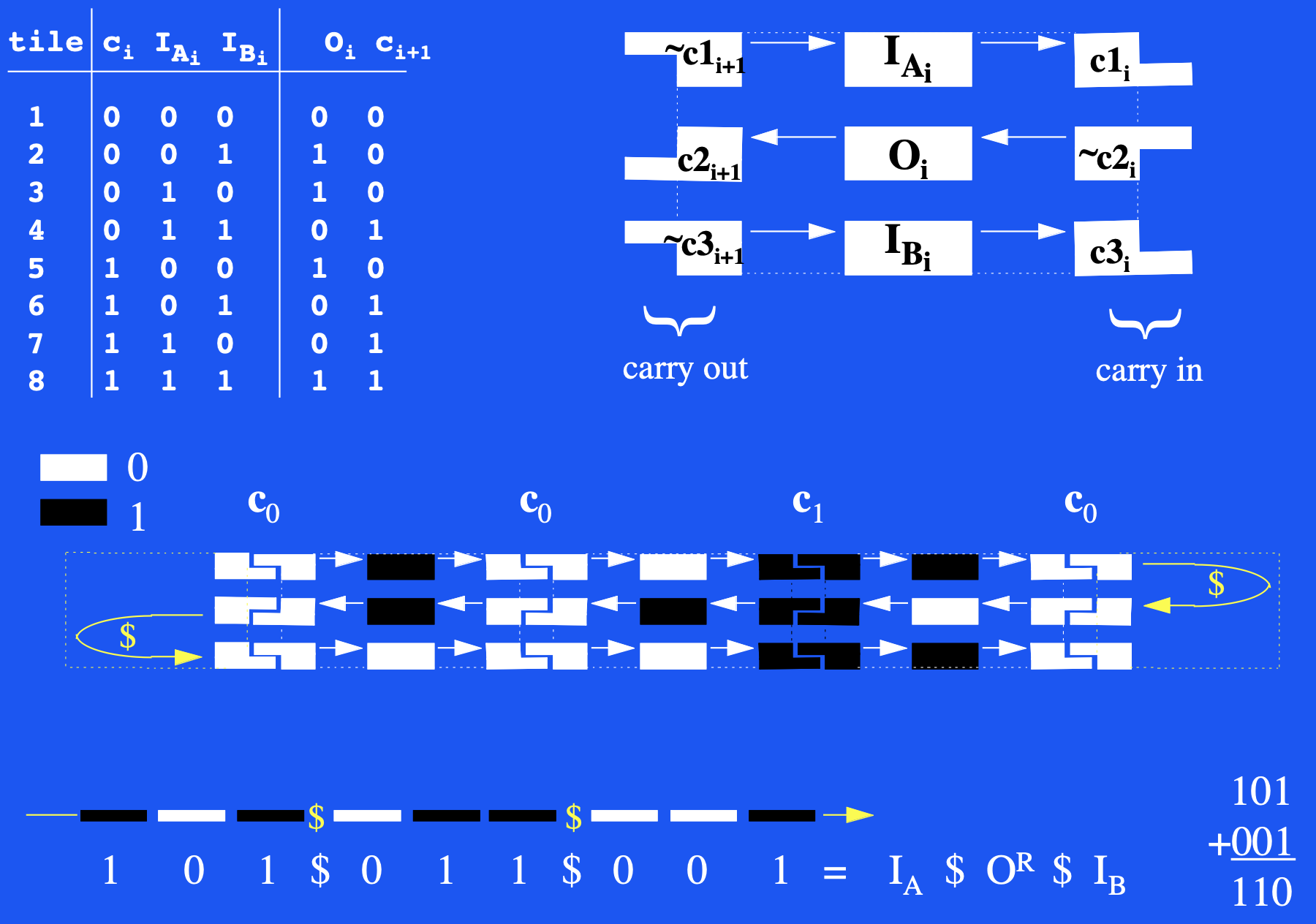
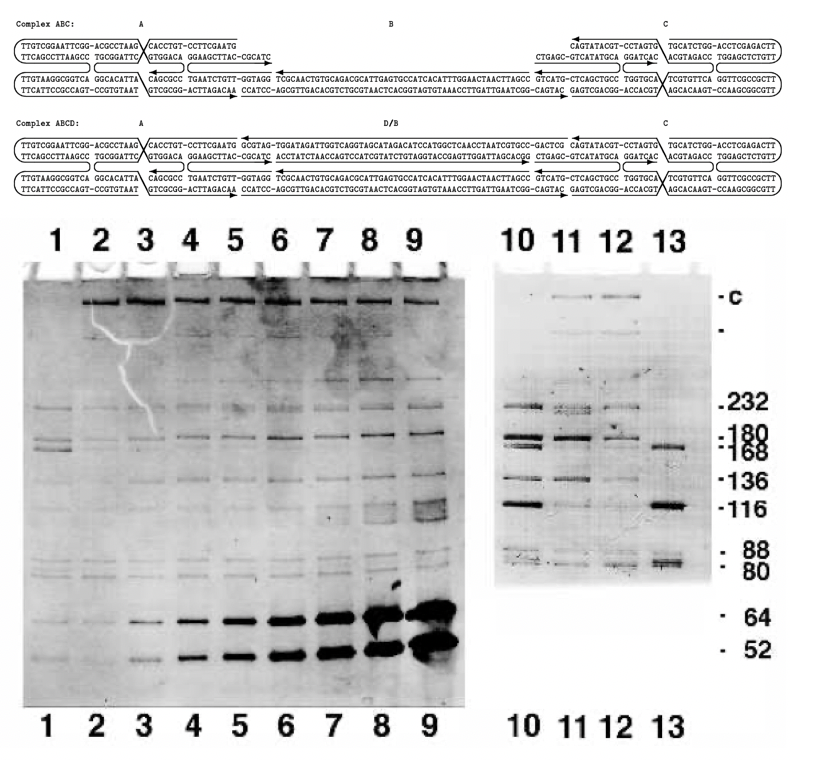
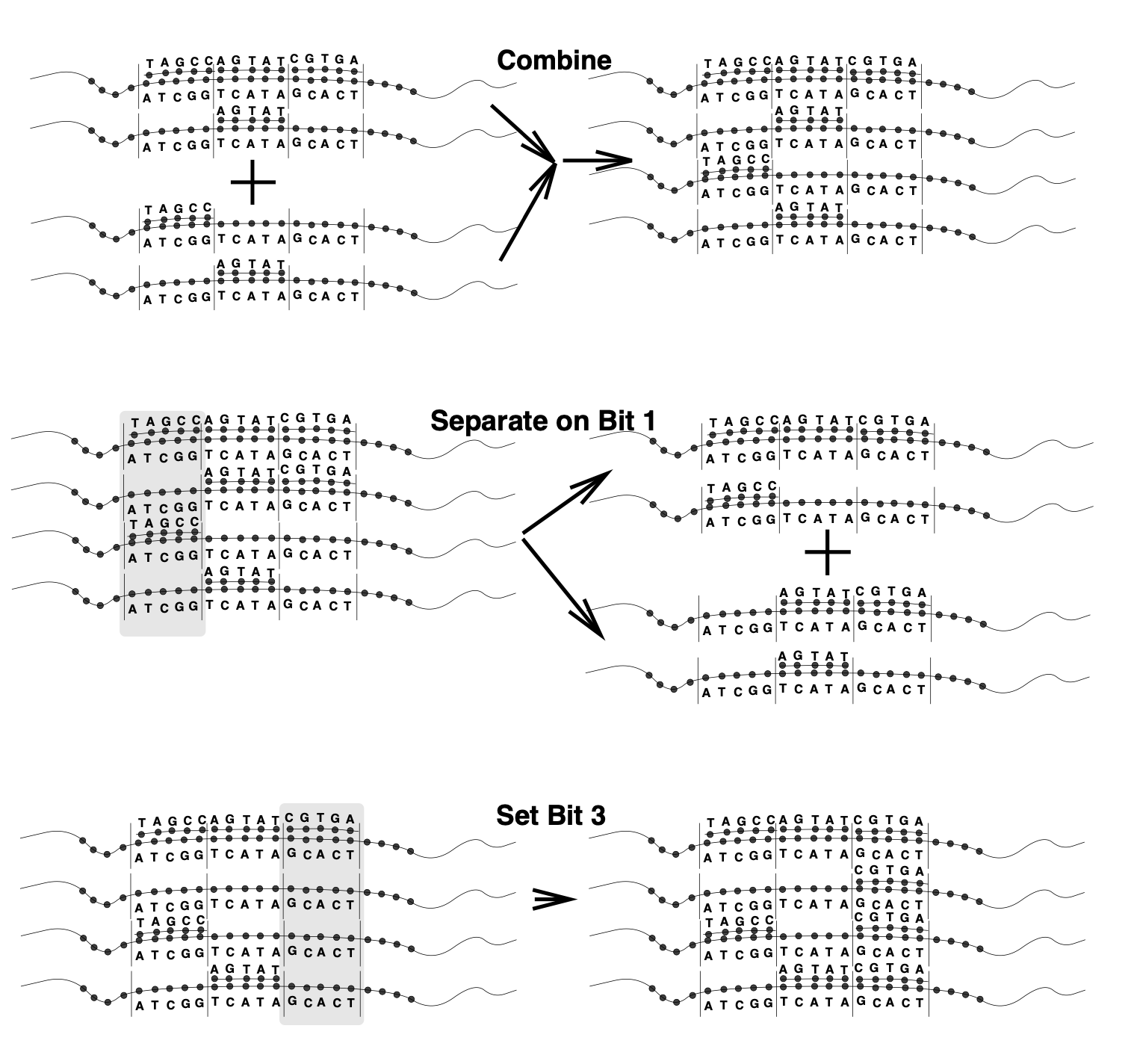
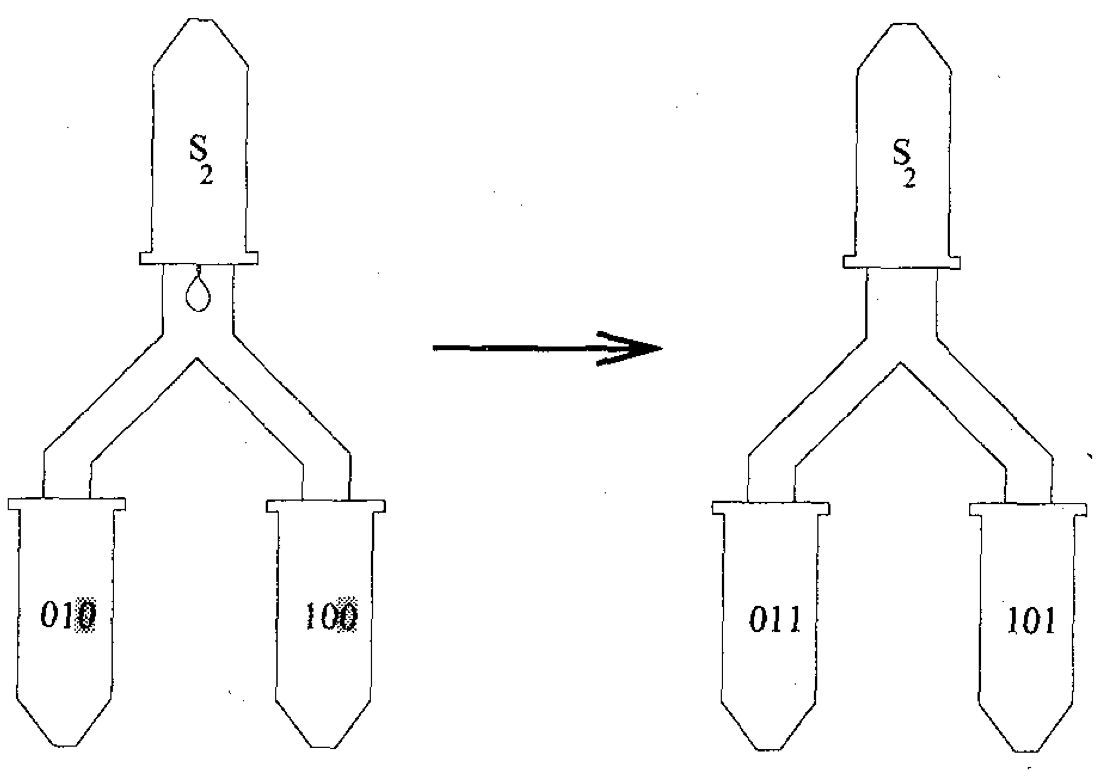
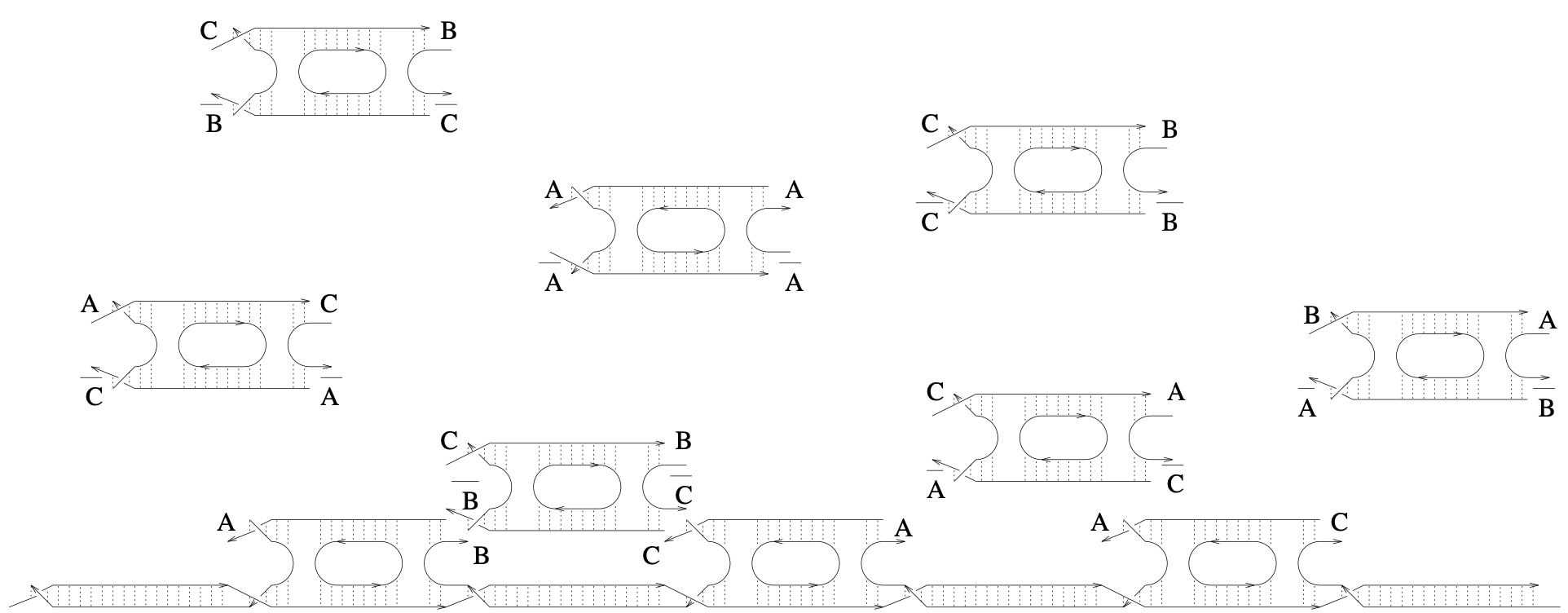
Aidan Zentner, Ethan V. Halingstad, Cameron Chalk, Michael P. Brenner, Arvind Murugan, Erik Winfree, and Krishna Shrinivas.
 |
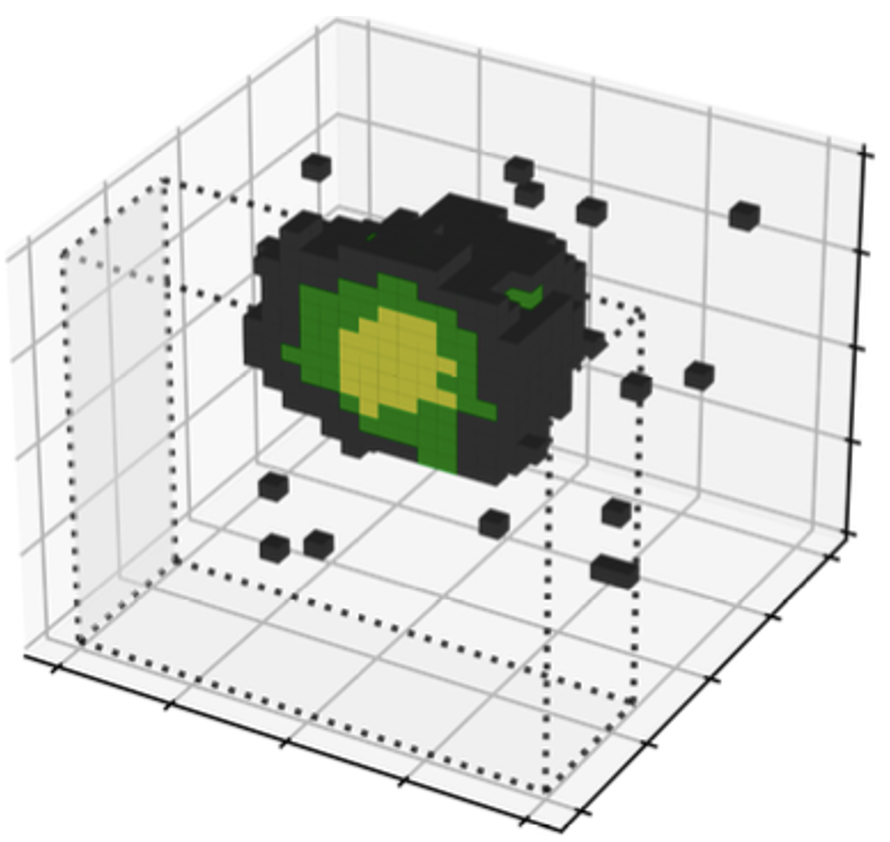
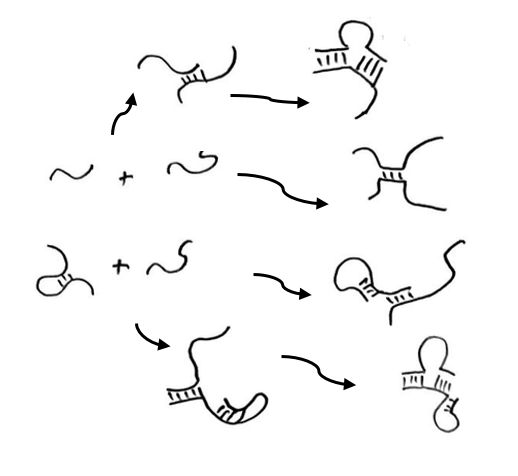
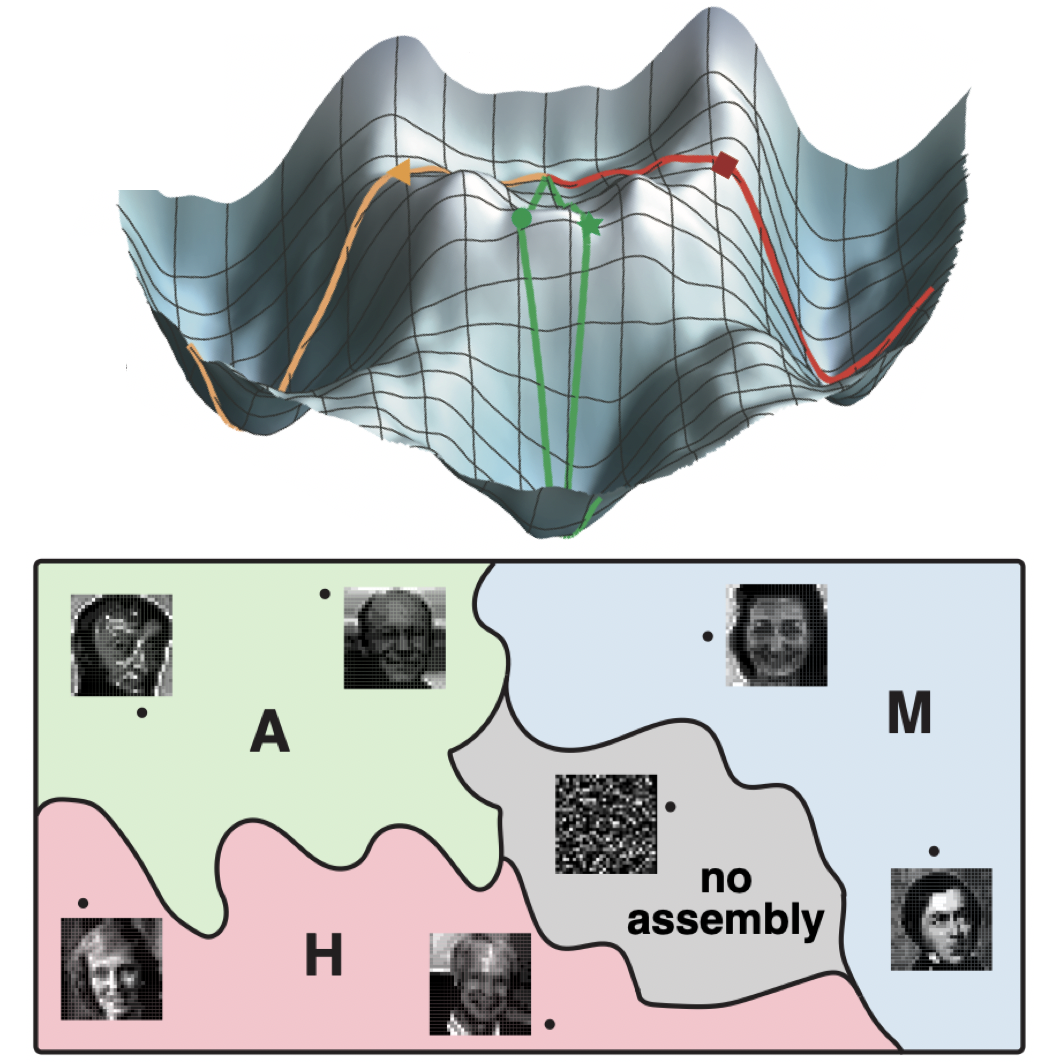
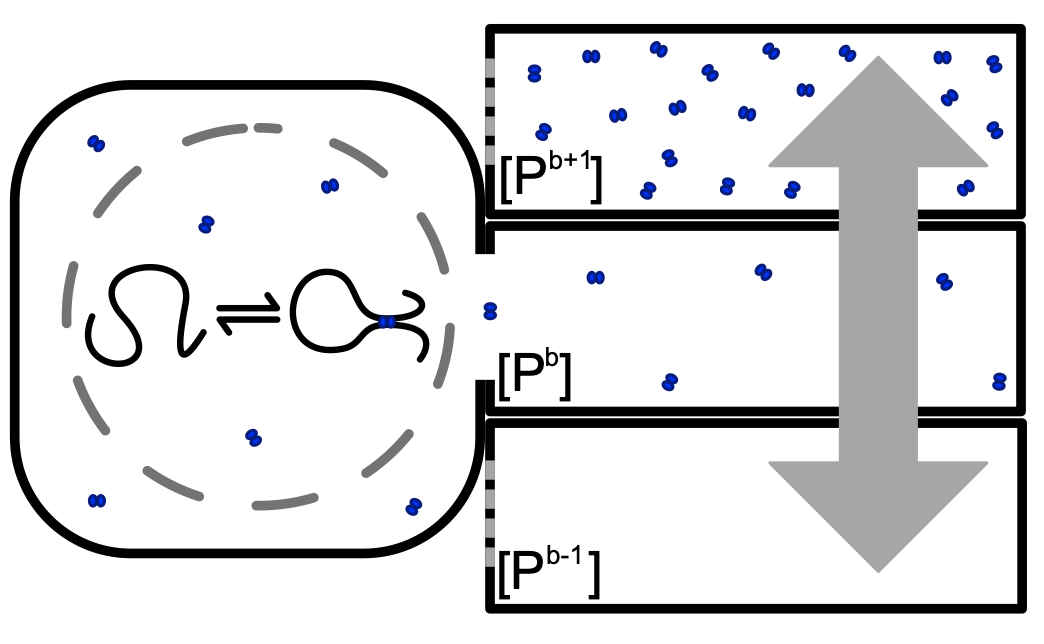
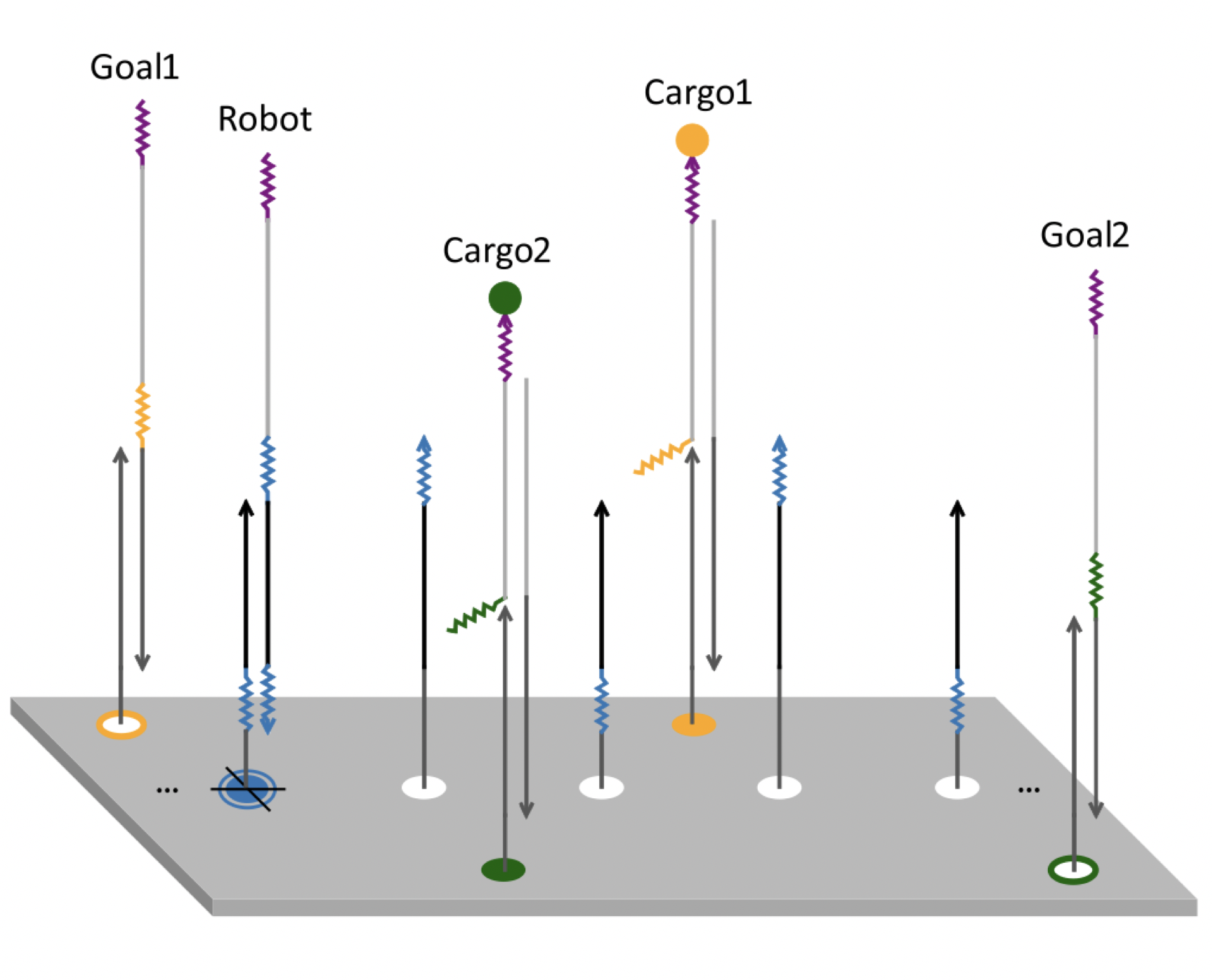
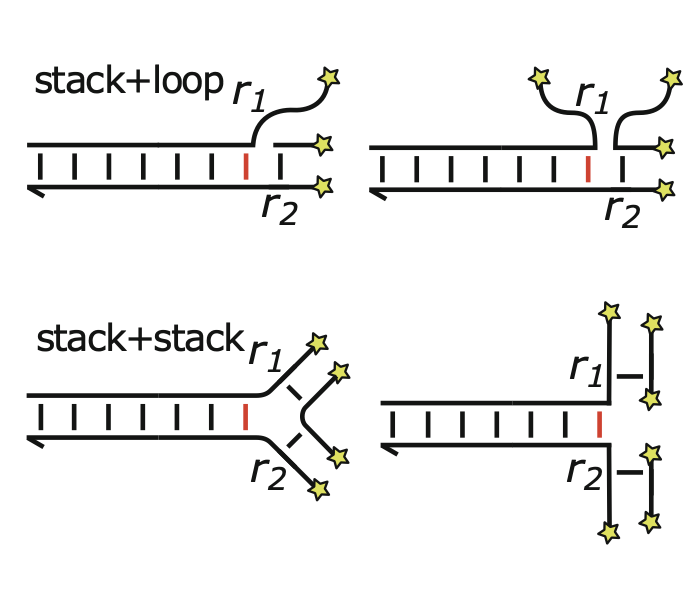
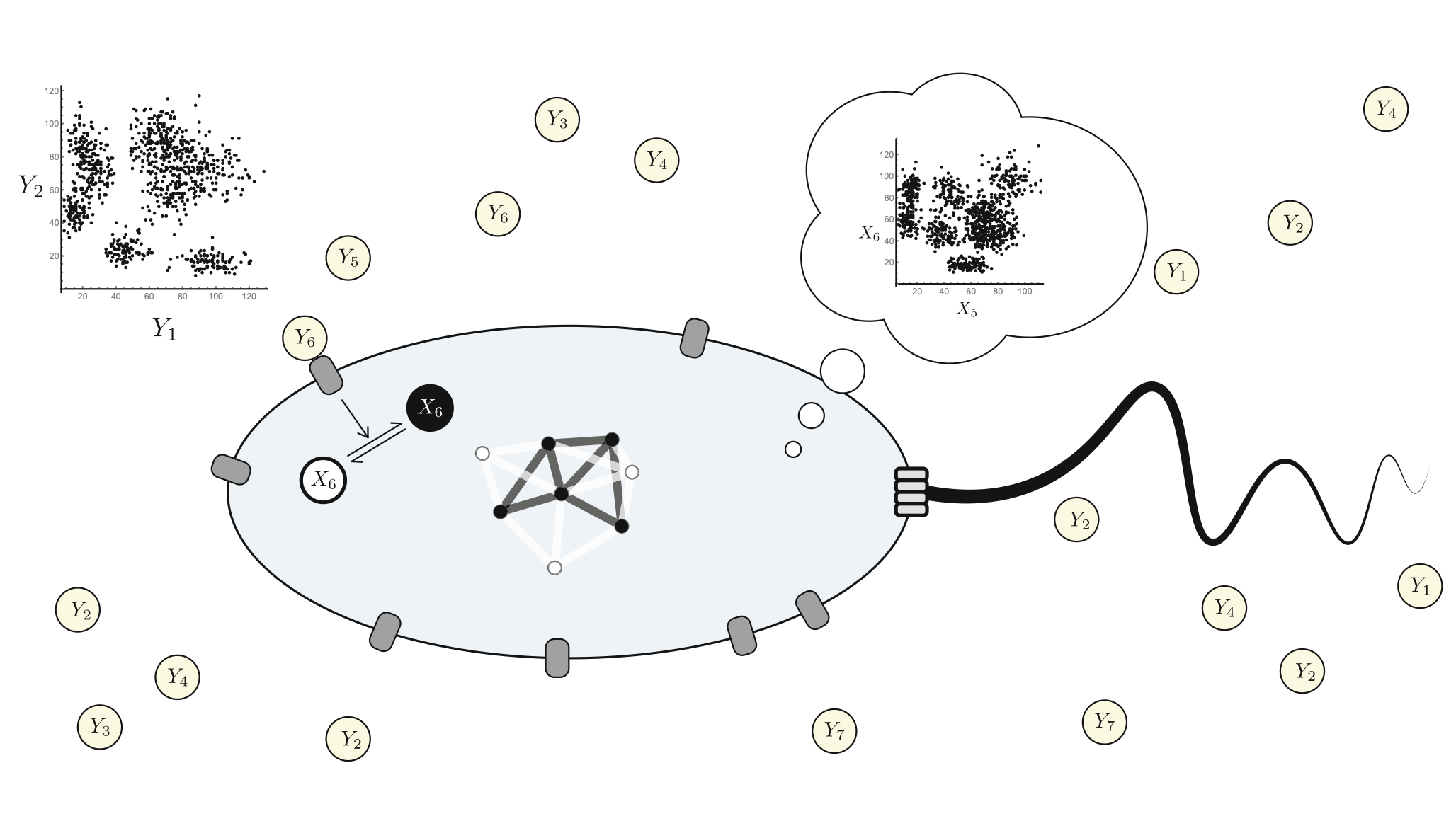
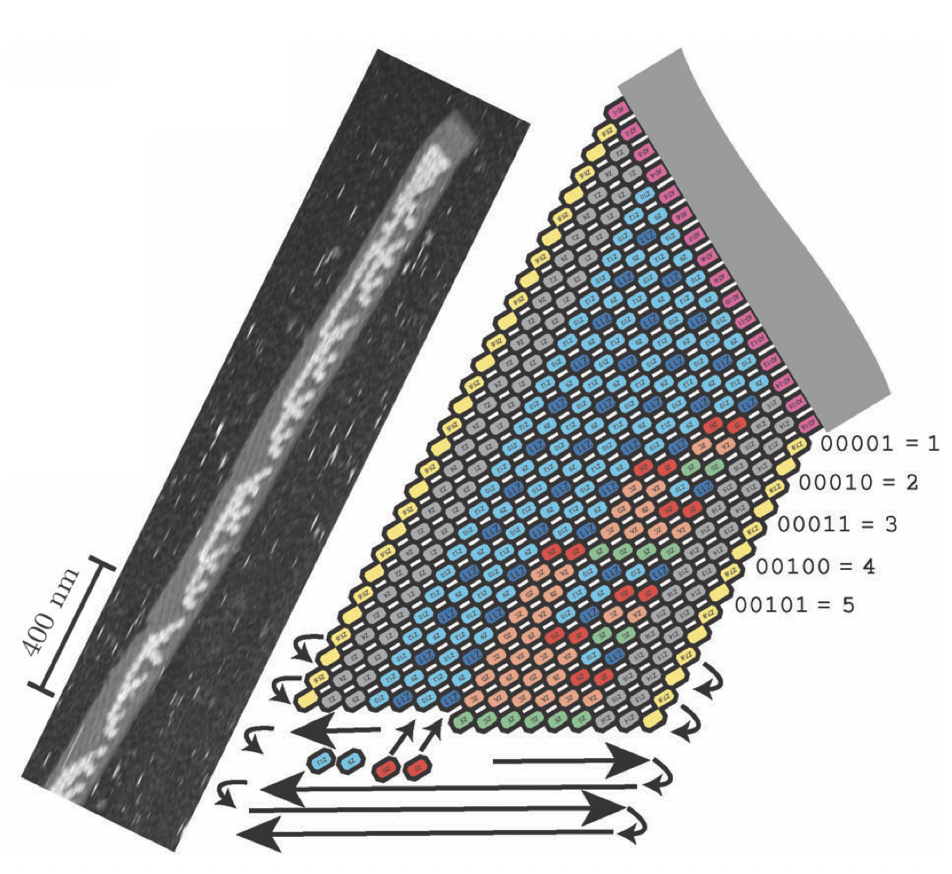
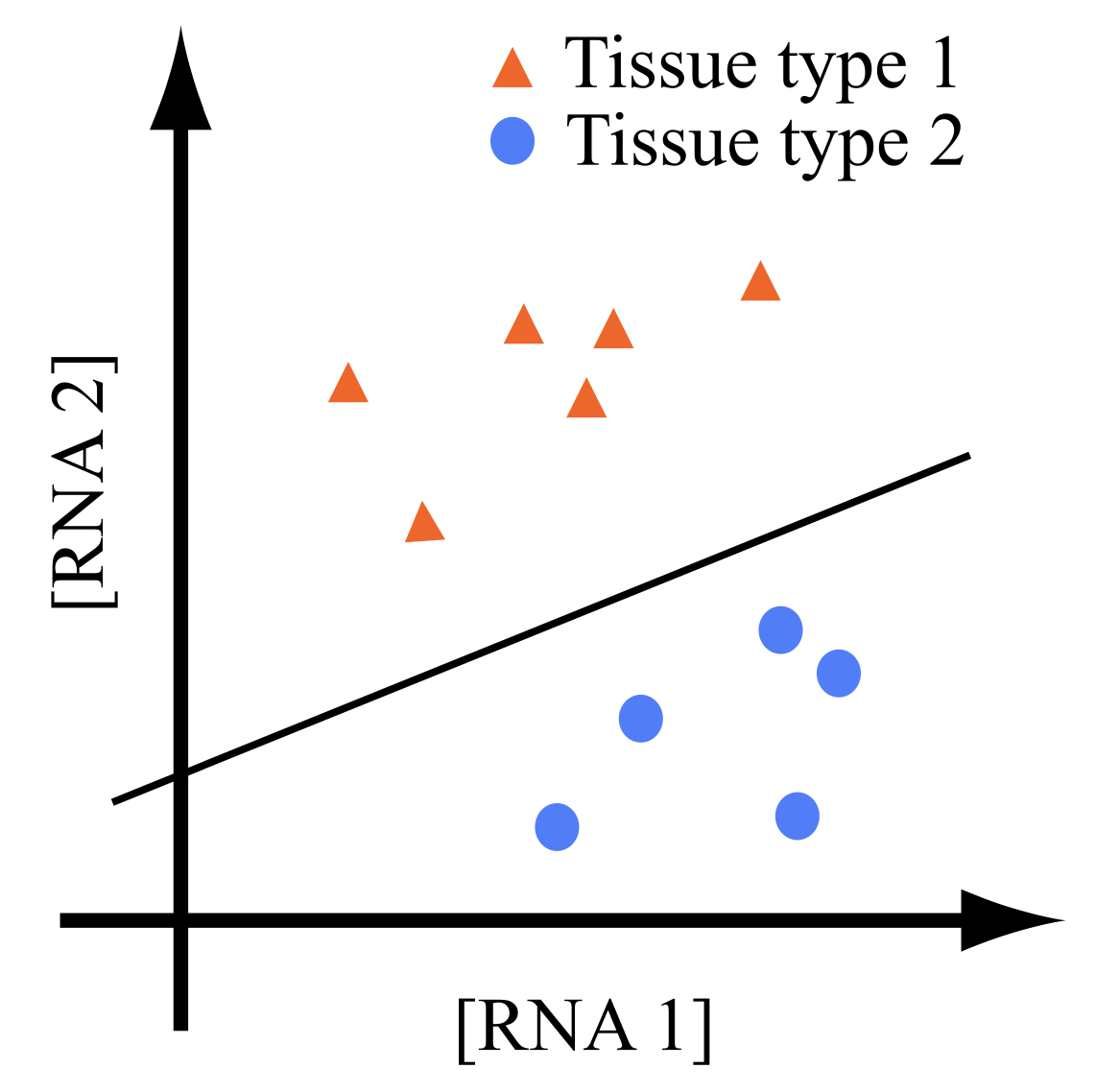
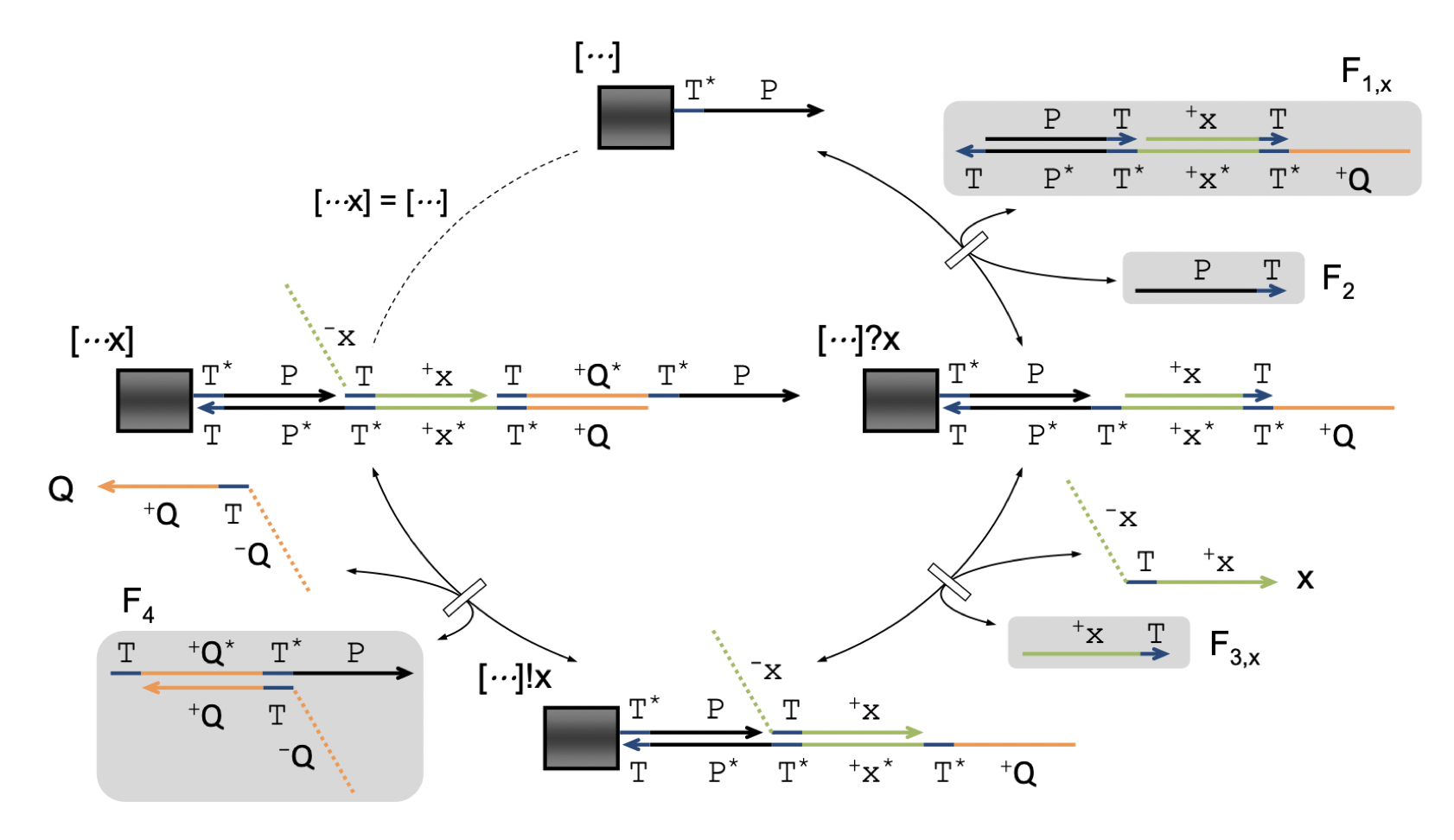
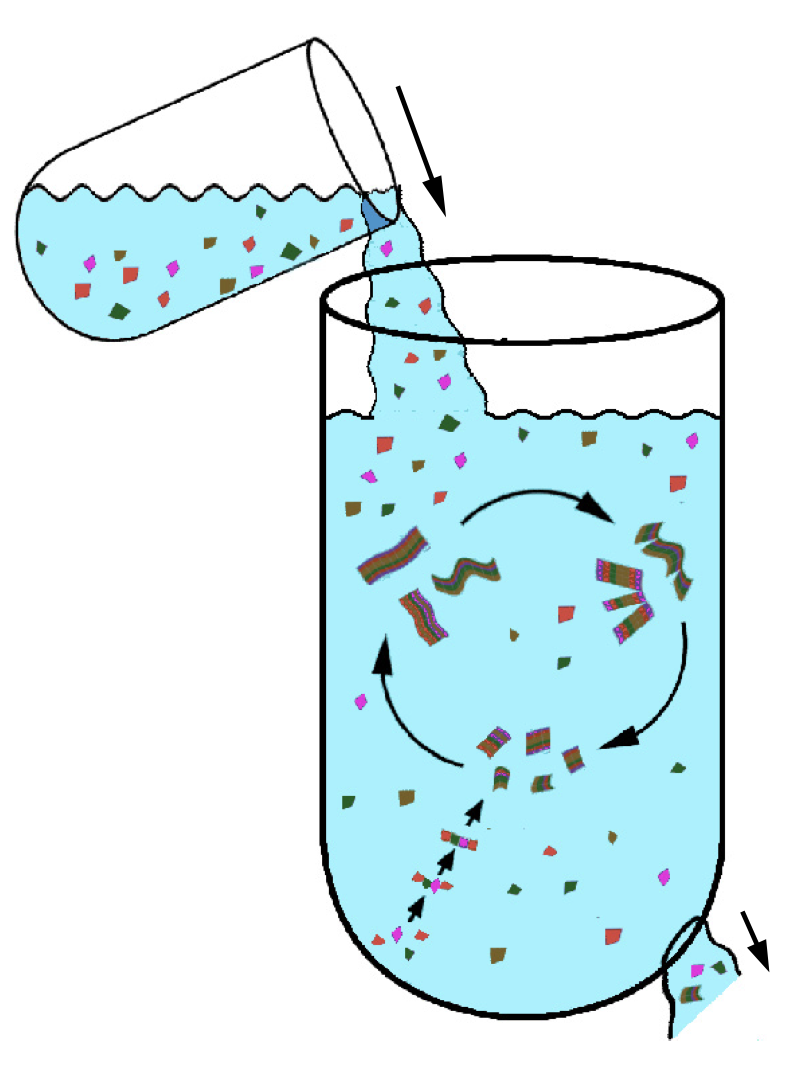
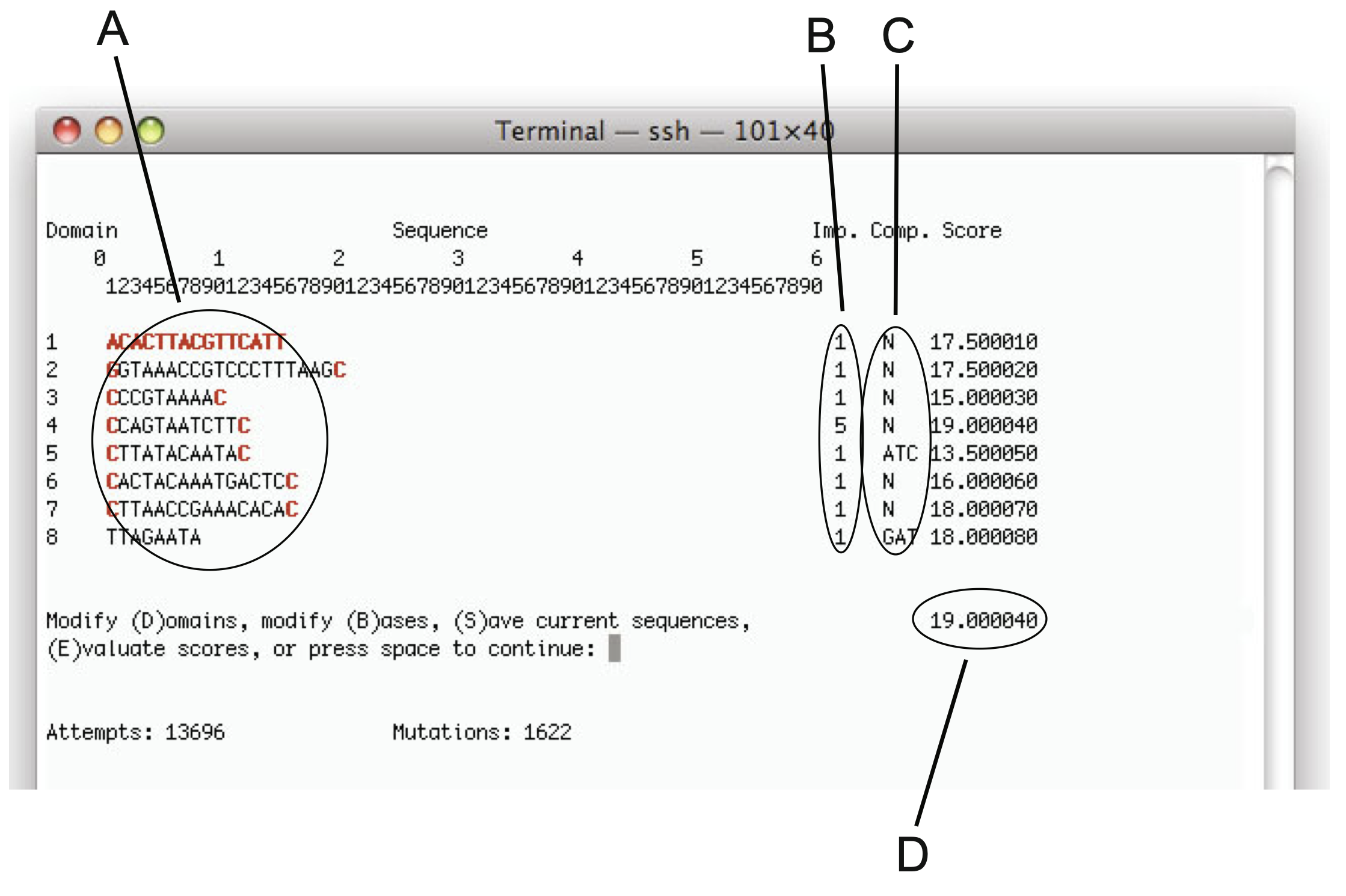
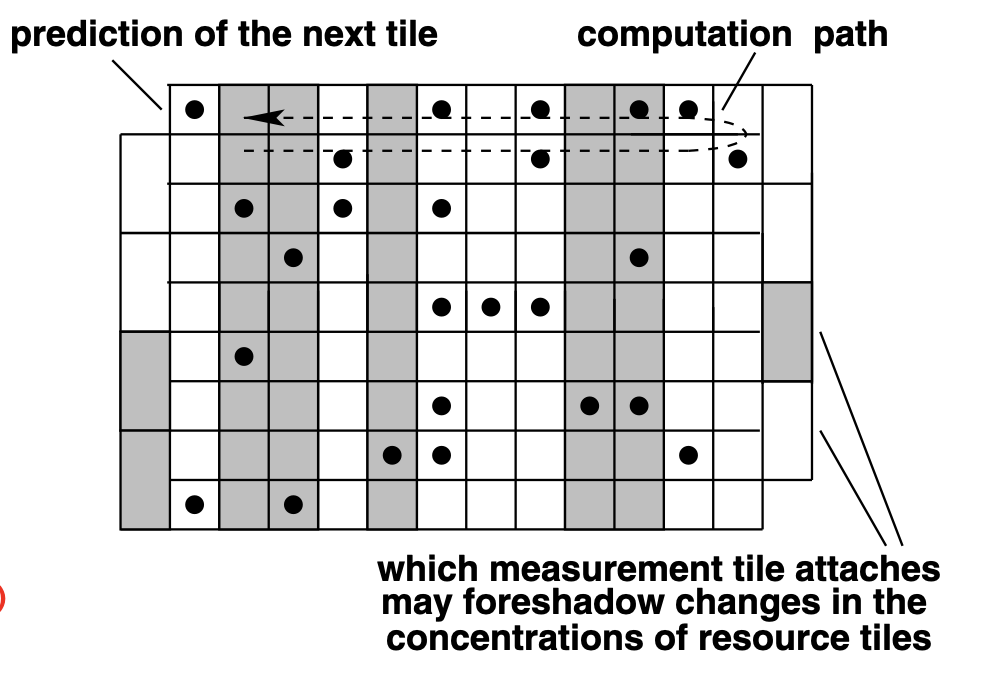
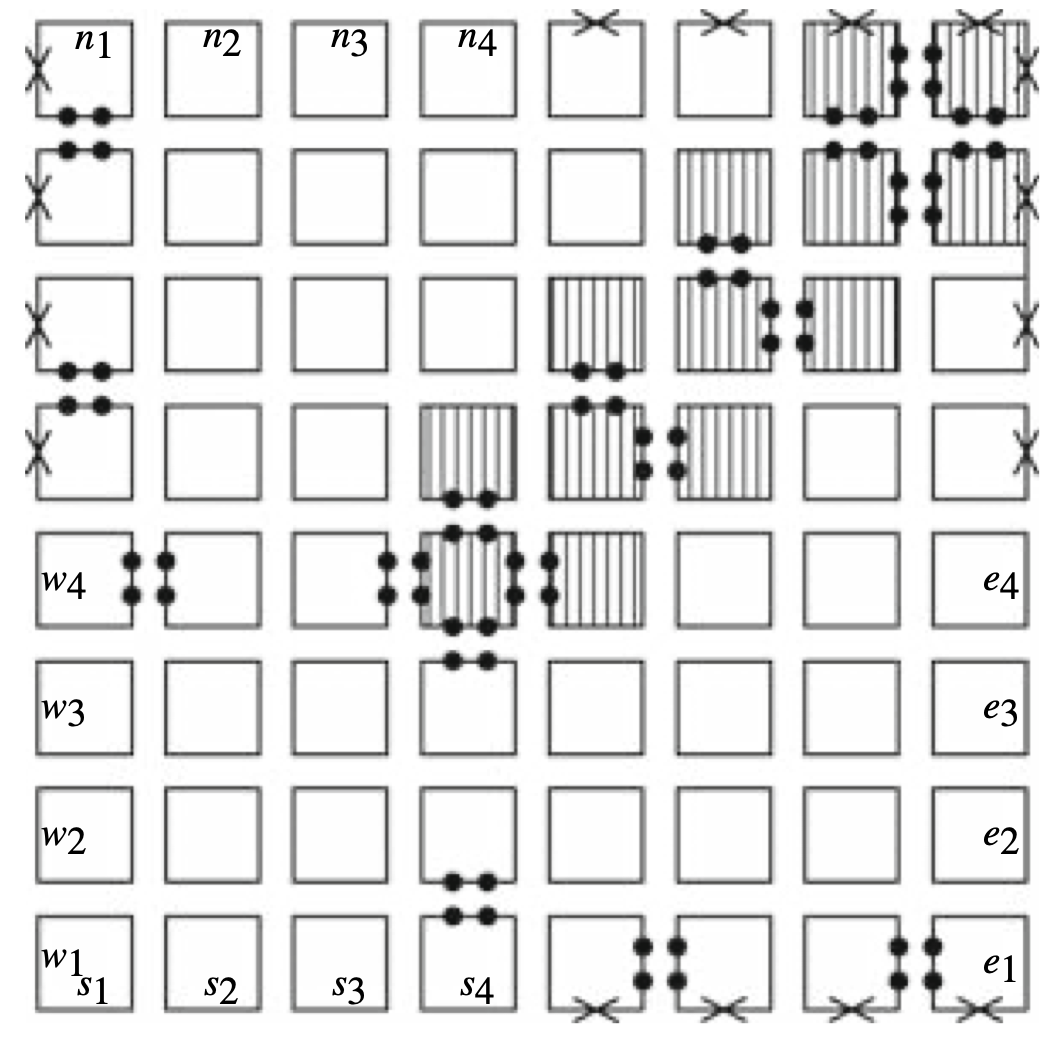
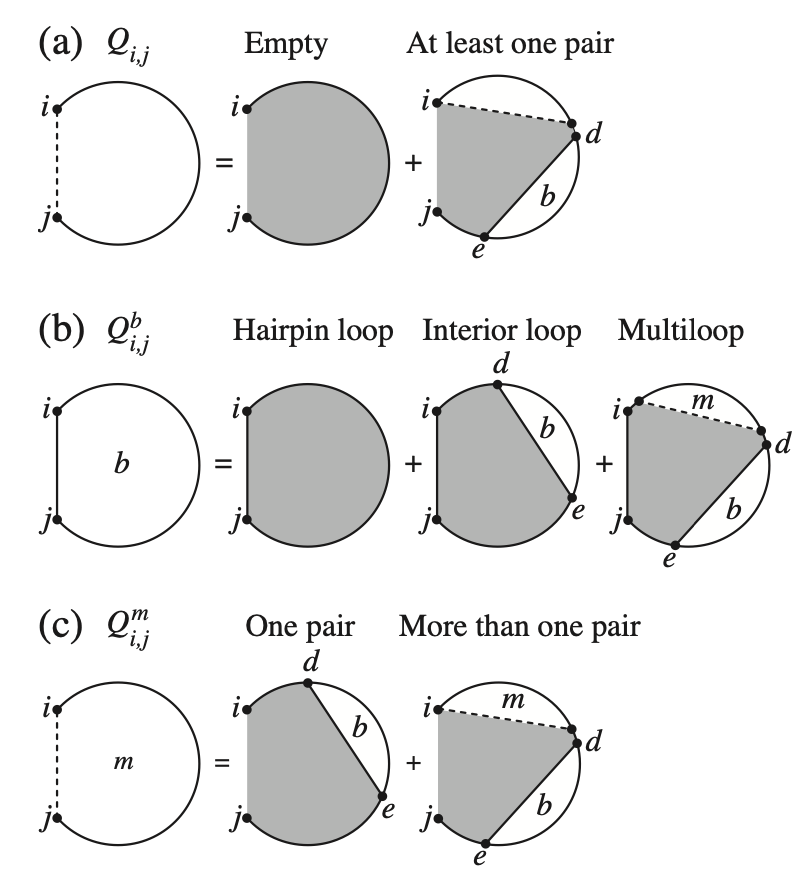
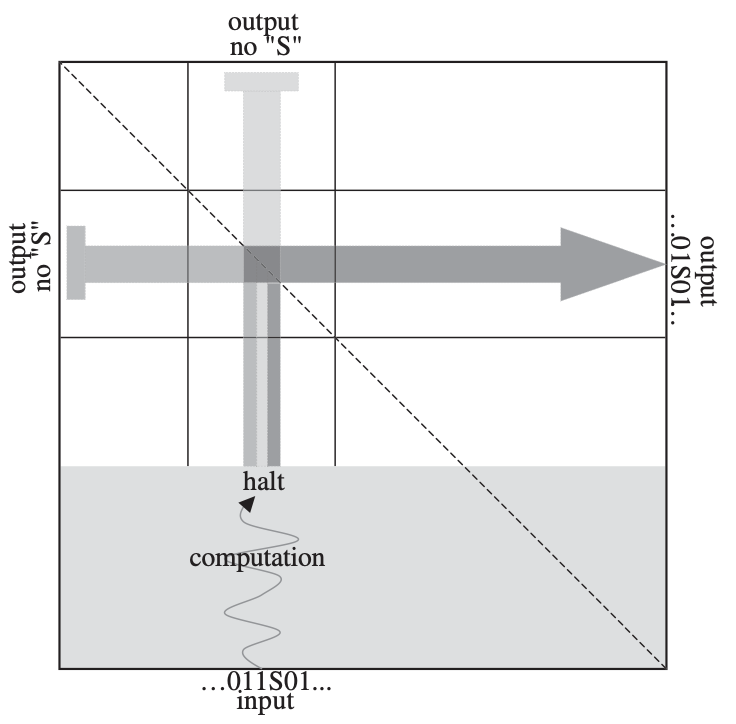
A flock of green parrots descends on a jacaranda tree. Why that tree? Some might call it swarm dynamics: a few birds decide to alight, others pass by, a few more join, some peel away, until, amid a cacophony of squawks, the whole flock settles. This is how collective decision-making works, unifying the inclinations of a hundred bird brains, not as a linear average, but as a nonlinear all-or-none. And so we have a green-and-purple tree in Pasadena in June... A jumble of transcription factors colocalize on a genomic locus. Why that locus? Some might call it phase separation: a few molecules stick to a favorable site, most drift past, a few more bind to the first, others fall off, until the balance of Brownian jostling tips and a droplet forms. This is how collective decision-making works, unifying the preferences of a thousand molecules, not as a linear average, but as a nonlinear all-or-none. And so we have dewdrops on the genome... |